Bayesian regularization of empirical MDPs
Paper and Code
Aug 03, 2022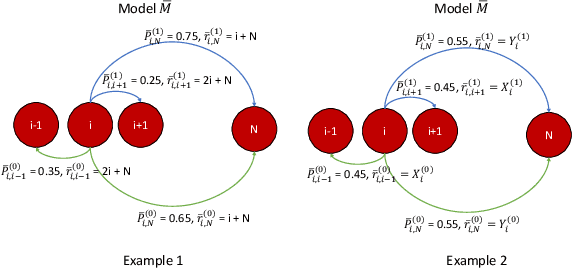
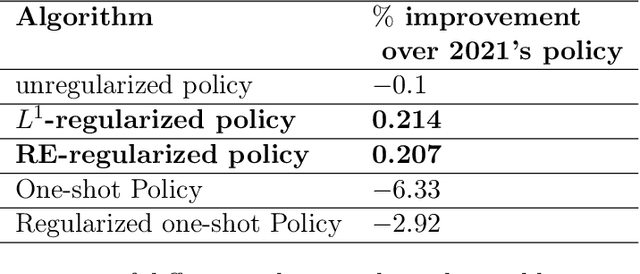
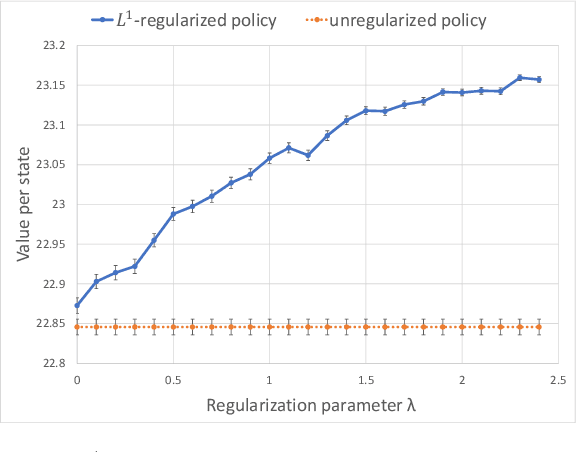
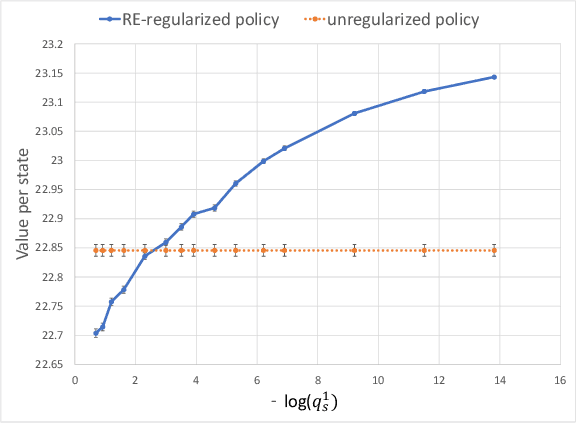
In most applications of model-based Markov decision processes, the parameters for the unknown underlying model are often estimated from the empirical data. Due to noise, the policy learnedfrom the estimated model is often far from the optimal policy of the underlying model. When applied to the environment of the underlying model, the learned policy results in suboptimal performance, thus calling for solutions with better generalization performance. In this work we take a Bayesian perspective and regularize the objective function of the Markov decision process with prior information in order to obtain more robust policies. Two approaches are proposed, one based on $L^1$ regularization and the other on relative entropic regularization. We evaluate our proposed algorithms on synthetic simulations and on real-world search logs of a large scale online shopping store. Our results demonstrate the robustness of regularized MDP policies against the noise present in the models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge