Bayesian Group Factor Analysis
Paper and Code
Oct 14, 2011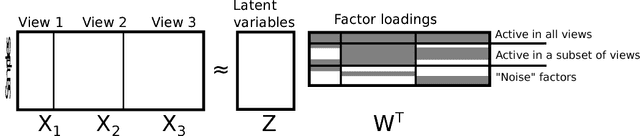
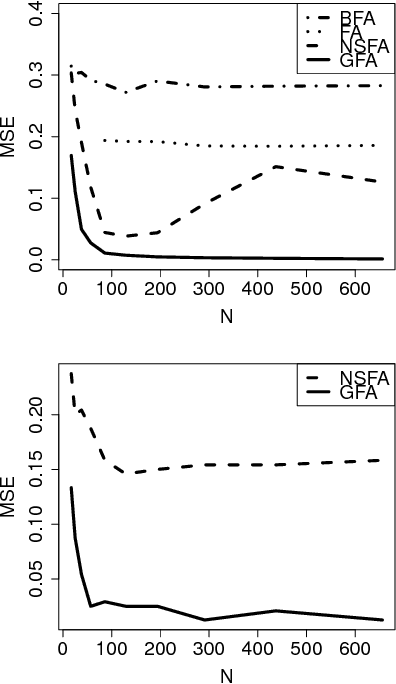
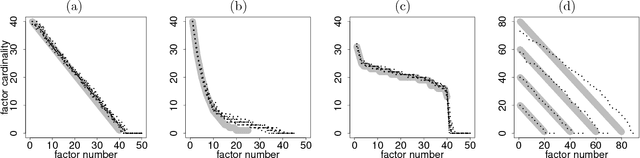
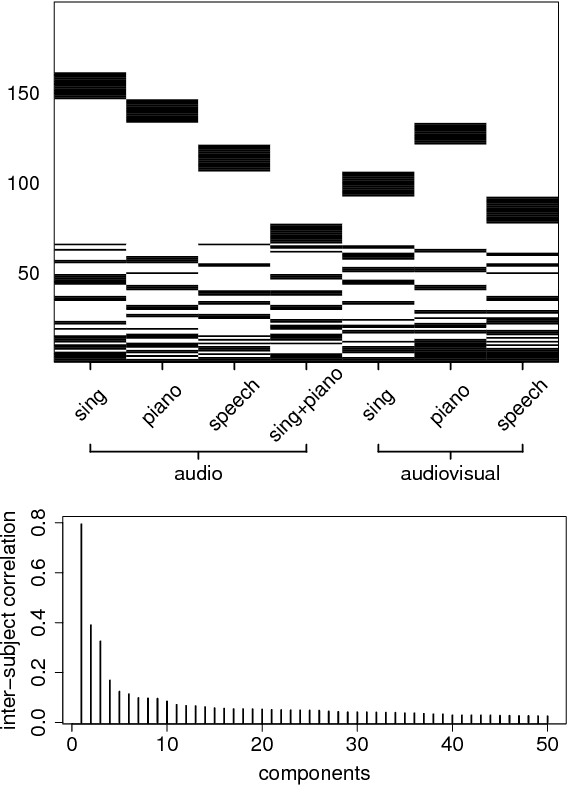
We introduce a factor analysis model that summarizes the dependencies between observed variable groups, instead of dependencies between individual variables as standard factor analysis does. A group may correspond to one view of the same set of objects, one of many data sets tied by co-occurrence, or a set of alternative variables collected from statistics tables to measure one property of interest. We show that by assuming group-wise sparse factors, active in a subset of the sets, the variation can be decomposed into factors explaining relationships between the sets and factors explaining away set-specific variation. We formulate the assumptions in a Bayesian model which provides the factors, and apply the model to two data analysis tasks, in neuroimaging and chemical systems biology.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge