Bayesian Approaches to Distribution Regression
Paper and Code
Feb 22, 2018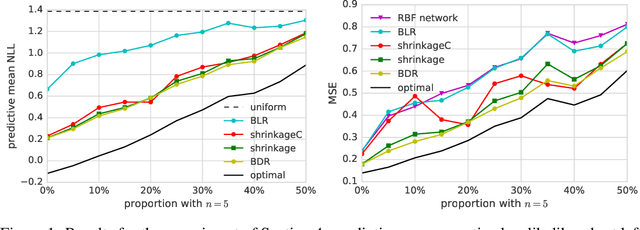
Distribution regression has recently attracted much interest as a generic solution to the problem of supervised learning where labels are available at the group level, rather than at the individual level. Current approaches, however, do not propagate the uncertainty in observations due to sampling variability in the groups. This effectively assumes that small and large groups are estimated equally well, and should have equal weight in the final regression. We account for this uncertainty with a Bayesian distribution regression formalism, improving the robustness and performance of the model when group sizes vary. We frame our models in a neural network style, allowing for simple MAP inference using backpropagation to learn the parameters, as well as MCMC-based inference which can fully propagate uncertainty. We demonstrate our approach on illustrative toy datasets, as well as on a challenging problem of predicting age from images.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge