Bayes Point Rule Set Learning
Paper and Code
Apr 11, 2022
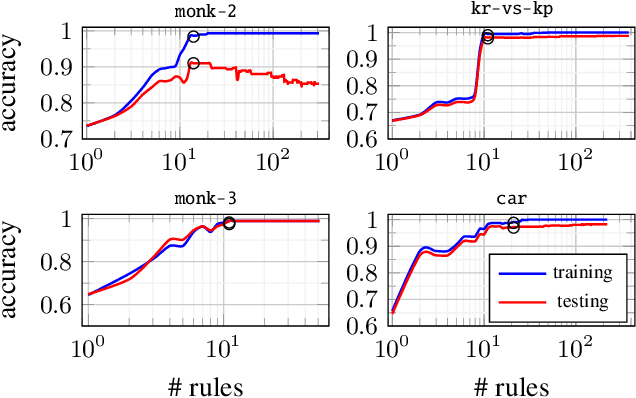

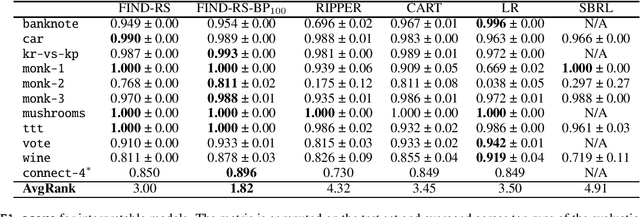
Interpretability is having an increasingly important role in the design of machine learning algorithms. However, interpretable methods tend to be less accurate than their black-box counterparts. Among others, DNFs (Disjunctive Normal Forms) are arguably the most interpretable way to express a set of rules. In this paper, we propose an effective bottom-up extension of the popular FIND-S algorithm to learn DNF-type rulesets. The algorithm greedily finds a partition of the positive examples. The produced DNF is a set of conjunctive rules, each corresponding to the most specific rule consistent with a part of positive and all negative examples. We also propose two principled extensions of this method, approximating the Bayes Optimal Classifier by aggregating DNF decision rules. Finally, we provide a methodology to significantly improve the explainability of the learned rules while retaining their generalization capabilities. An extensive comparison with state-of-the-art symbolic and statistical methods on several benchmark data sets shows that our proposal provides an excellent balance between explainability and accuracy.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge