Bayes-optimal Hierarchical Classification over Asymmetric Tree-Distance Loss
Paper and Code
Feb 17, 2018
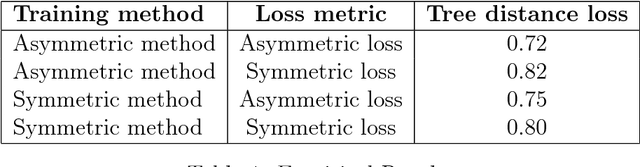
Hierarchical classification is supervised multi-class classification problem over the set of class labels organized according to a hierarchy. In this report, we study the work by Ramaswamy et. al. on hierarchical classification over symmetric tree distance loss. We extend the consistency of hierarchical classification algorithm over asymmetric tree distance loss. We design a $\mathcal{O}(nk\log{}n)$ algorithm to find Bayes optimal classification for a k-ary tree as a hierarchy. We show that under reasonable assumptions over asymmetric loss function, the Bayes optimal classification over this asymmetric loss can be found in $\mathcal{O}(k\log{}n)$. We exploit this insight and attempt to extend the Ova-Cascade algorithm \citet{ramaswamy2015convex} for hierarchical classification over the asymmetric loss.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge