Ball k-means
Paper and Code
May 02, 2020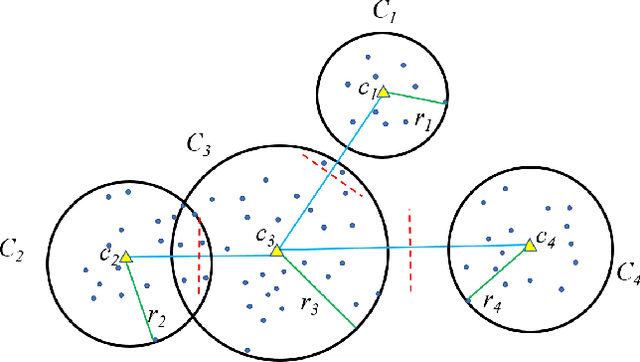
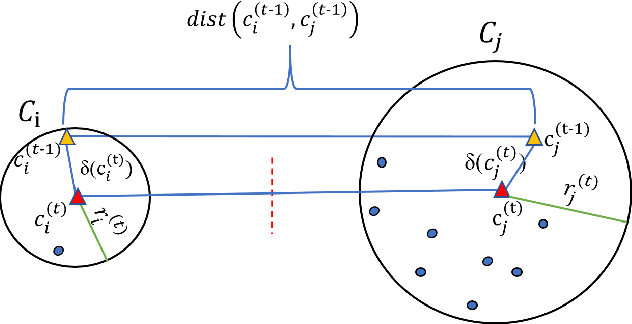
This paper presents a novel accelerated exact k-means algorithm called the Ball k-means algorithm, which uses a ball to describe a cluster, focusing on reducing the point-centroid distance computation. The Ball k-means can accurately find the neighbor clusters for each cluster resulting distance computations only between a point and its neighbor clusters' centroids instead of all centroids. Moreover, each cluster can be divided into a stable area and an active area, and the later one can be further divided into annulus areas. The assigned cluster of the points in the stable area is not changed in the current iteration while the points in the annulus area will be adjusted within a few neighbor clusters in the current iteration. Also, there are no upper or lower bounds in the proposed Ball k-means. Furthermore, reducing centroid-centroid distance computation between iterations makes it efficient for large k clustering. The fast speed, no extra parameters and simple design of the Ball k-means make it an all-around replacement of the naive k-means algorithm.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge