Backprop Evolution
Paper and Code
Aug 08, 2018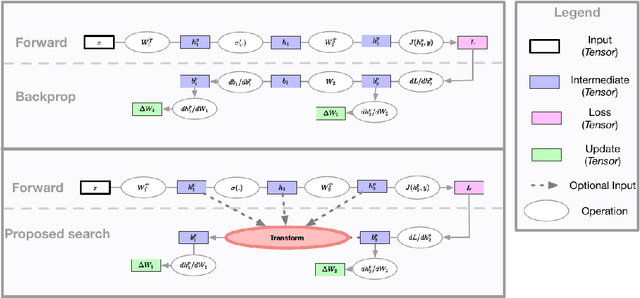
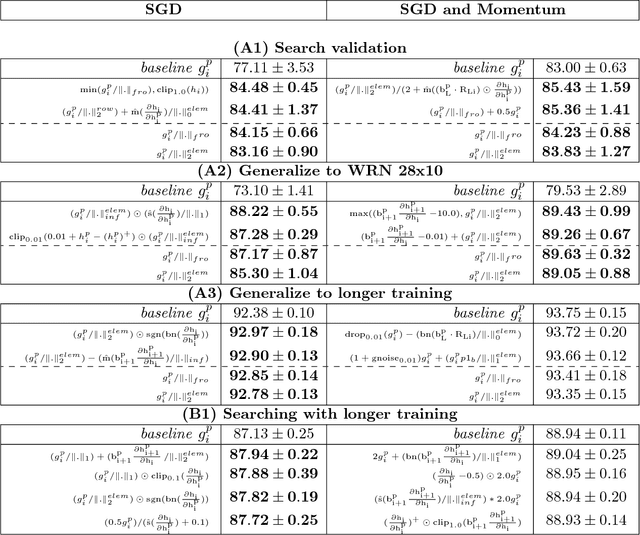
The back-propagation algorithm is the cornerstone of deep learning. Despite its importance, few variations of the algorithm have been attempted. This work presents an approach to discover new variations of the back-propagation equation. We use a domain specific lan- guage to describe update equations as a list of primitive functions. An evolution-based method is used to discover new propagation rules that maximize the generalization per- formance after a few epochs of training. We find several update equations that can train faster with short training times than standard back-propagation, and perform similar as standard back-propagation at convergence.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge