Back-propagation through Signal Temporal Logic Specifications: Infusing Logical Structure into Gradient-Based Methods

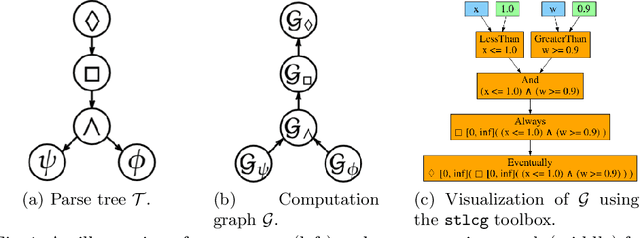
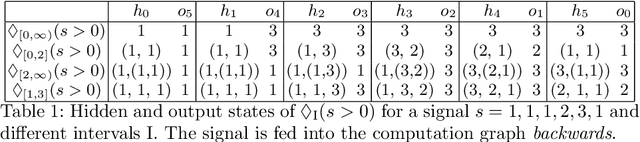
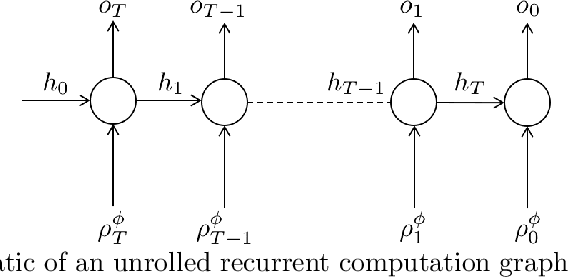
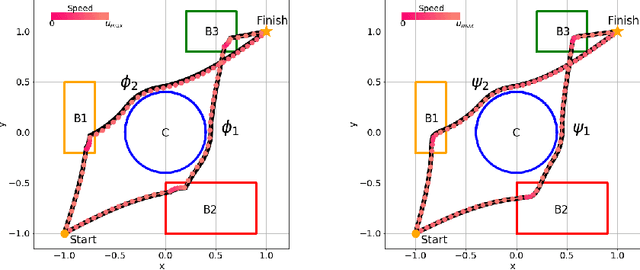
This paper presents a technique, named STLCG, to compute the quantitative semantics of Signal Temporal Logic (STL) formulas using computation graphs. STLCG provides a platform which enables the incorporation of logical specifications into robotics problems that benefit from gradient-based solutions. Specifically, STL is a powerful and expressive formal language that can specify spatial and temporal properties of signals generated by both continuous and hybrid systems. The quantitative semantics of STL provide a robustness metric, i.e., how much a signal satisfies or violates an STL specification. In this work, we devise a systematic methodology for translating STL robustness formulas into computation graphs. With this representation, and by leveraging off-the-shelf automatic differentiation tools, we are able to back-propagate through STL robustness formulas and hence enable a natural and easy-to-use integration with many gradient-based approaches used in robotics. We demonstrate, through examples stemming from various robotics applications, that STLCG is versatile, computationally efficient, and capable of injecting human-domain knowledge into the problem formulation.