Avoiding Dense and Dynamic Obstacles in Enclosed Spaces: Application to Moving in Crowds
Paper and Code
Jun 04, 2021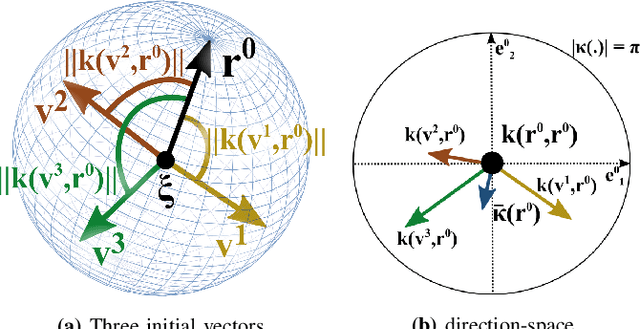
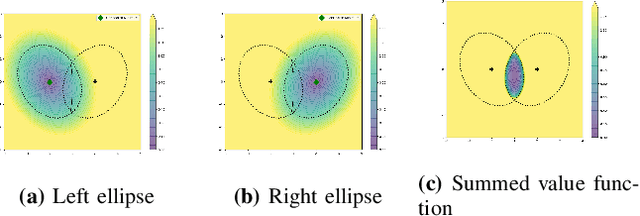

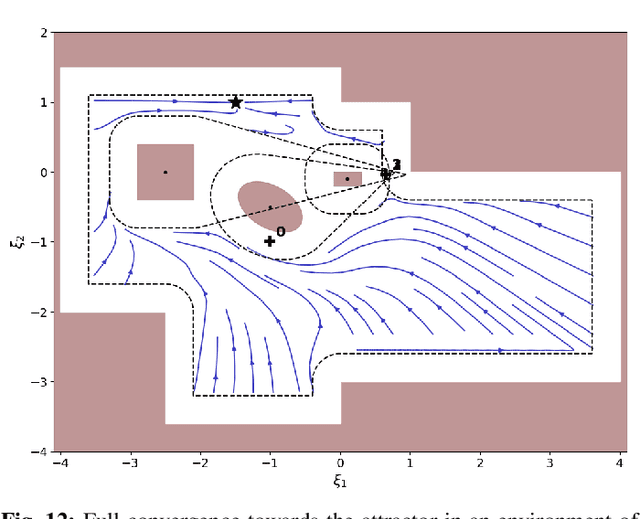
This paper presents a closed-form approach to constrain a flow within a given volume and around objects. The flow is guaranteed to converge and to stop at a single fixed point. We show that the obstacle avoidance problem can be inverted to enforce that the flow remains enclosed within a volume defined by a polygonal surface. We formally guarantee that such a flow will never contact the boundaries of the enclosing volume and obstacles, and will asymptotically converge towards an attractor. We further create smooth motion fields around obstacles with edges (e.g. tables). Both obstacles and enclosures may be time-varying, i.e. moving, expanding and shrinking. The technique enables a robot to navigate within an enclosed corridor while avoiding static and moving obstacles. It was applied on an autonomous robot (QOLO) in a static complex indoor environment, and also tested in simulations with dense crowds. The final proof of concept was performed in an outdoor environment in Lausanne. The QOLO-robot successfully traversed a marketplace in the center of town in presence of a diverse crowd with a non-uniform motion pattern.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge