Average Communication Rate for Event-Triggered Stochastic Control Systems

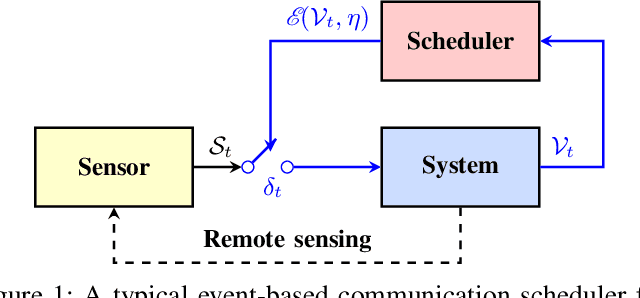
Quantification of the triggering rates of an event-triggered stochastic system with deterministic thresholds is a challenging problem due to the non-stationary nature of the system's stochastic processes. A typical example is the computation of the average communication rate (ACR) of the networked event-triggered stochastic control systems (ET-SCS) of which the communication of the sensor network is scheduled by whether a system variable of interest exceeds predefined constant thresholds. For such a system, a closed-loop effect emerges due to the interdependence between the system variable and the trigger of communication. This effect, commonly referred to as \textit{side information} by related work, distorts the stochastic distribution of the system variables and makes the ACR computation non-trivial. Previous work in this area used to over-simplify the computation by ignoring the side information and misusing a Gaussian distribution, which leads to approximated results. This paper proposes both analytical and numerical approaches to predict the exact ACR for an ET-SCS using a recursive model. Furthermore, we use theoretical analysis and a numerical study to qualitatively evaluate the deviation gap of the conventional approach that ignores the side information. The accuracy of our proposed method, alongside its comparison with the simplified results of the conventional approach, is validated by experimental studies. Our work is promising to benefit the efficient resource planning of networked control systems with limited communication resources by providing accurate ACR computation.