Automatically Composing Representation Transformations as a Means for Generalization

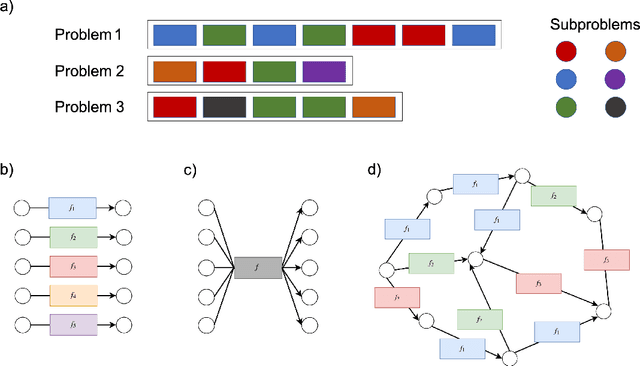
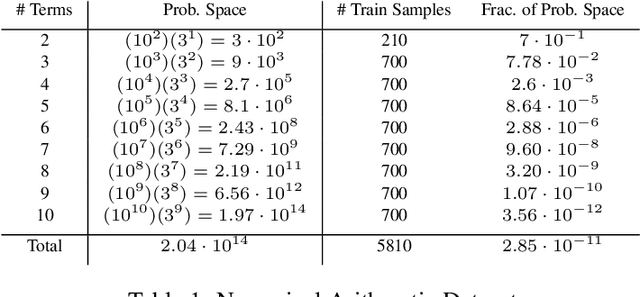
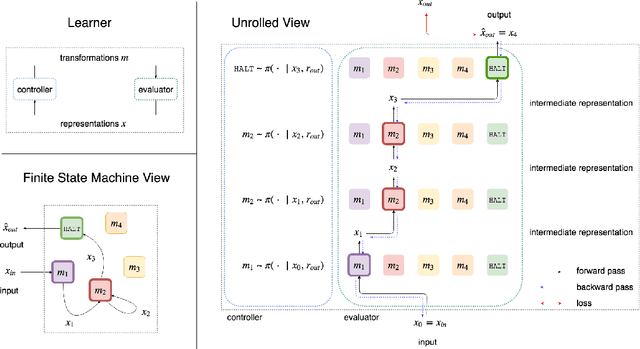
How can we build a learner that can capture the essence of what makes a hard problem more complex than a simple one, break the hard problem along characteristic lines into smaller problems it knows how to solve, and sequentially solve the smaller problems until the larger one is solved? To work towards this goal, we focus on learning to generalize in a particular family of problems that exhibit compositional and recursive structure: their solutions can be found by composing in sequence a set of reusable partial solutions. Our key idea is to recast the problem of generalization as a problem of learning algorithmic procedures: we can formulate a solution to this family as a sequential decision-making process over transformations between representations. Our formulation enables the learner to learn the structure and parameters of its own computation graph with sparse supervision, make analogies between problems by transforming one problem representation to another, and exploit modularity and reuse to scale to problems of varying complexity. Experiments on solving a variety of multilingual arithmetic problems demonstrate that our method discovers the hierarchical decomposition of a problem into its subproblems, generalizes out of distribution to unseen problem classes, and extrapolates to harder versions of the same problem, yielding a 10-fold reduction in sample complexity compared to a monolithic recurrent neural network.