Auto-DSP: Learning to Optimize Acoustic Echo Cancellers
Paper and Code
Oct 08, 2021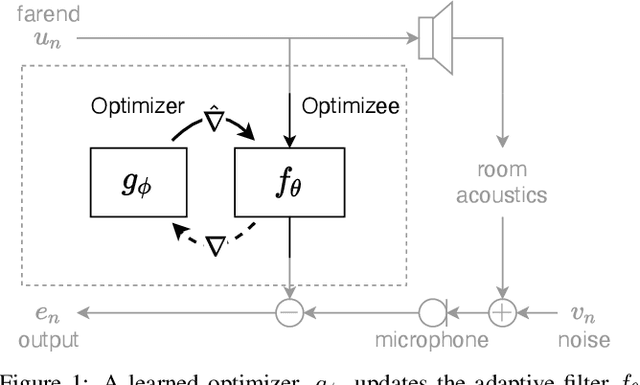
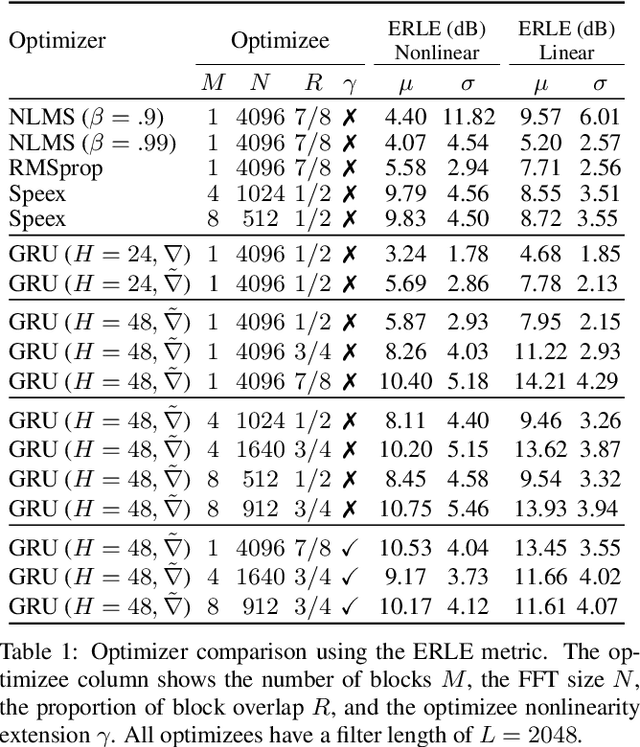
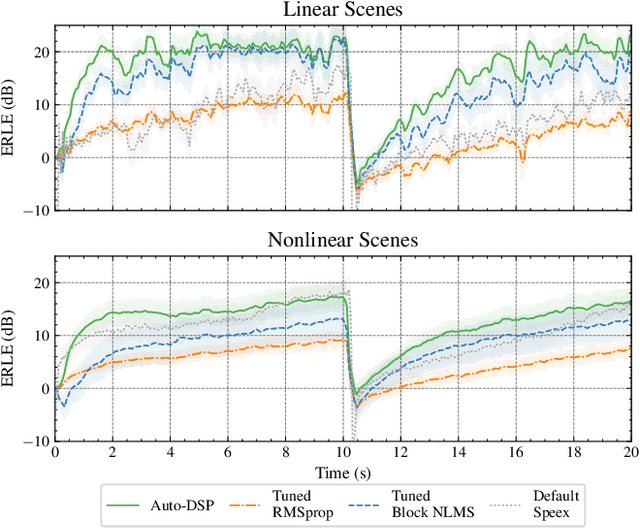
Adaptive filtering algorithms are commonplace in signal processing and have wide-ranging applications from single-channel denoising to multi-channel acoustic echo cancellation and adaptive beamforming. Such algorithms typically operate via specialized online, iterative optimization methods and have achieved tremendous success, but require expert knowledge, are slow to develop, and are difficult to customize. In our work, we present a new method to automatically learn adaptive filtering update rules directly from data. To do so, we frame adaptive filtering as a differentiable operator and train a learned optimizer to output a gradient descent-based update rule from data via backpropagation through time. We demonstrate our general approach on an acoustic echo cancellation task (single-talk with noise) and show that we can learn high-performing adaptive filters for a variety of common linear and non-linear multidelayed block frequency domain filter architectures. We also find that our learned update rules exhibit fast convergence, can optimize in the presence of nonlinearities, and are robust to acoustic scene changes despite never encountering any during training.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge