Asynchrony begets Momentum, with an Application to Deep Learning
Paper and Code
Nov 25, 2016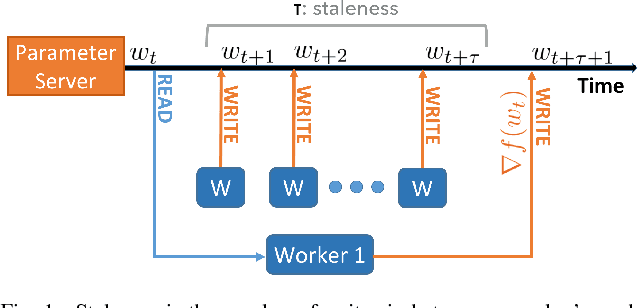

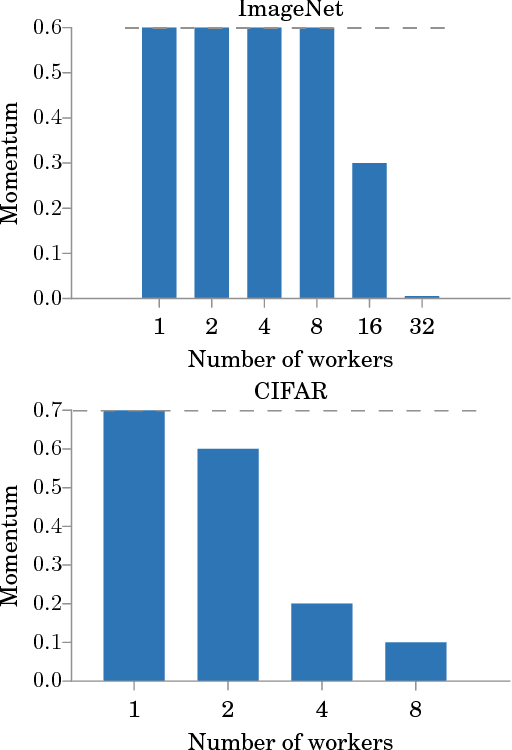
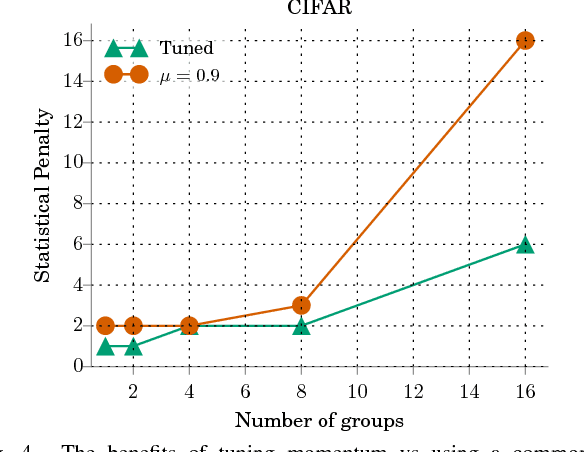
Asynchronous methods are widely used in deep learning, but have limited theoretical justification when applied to non-convex problems. We show that running stochastic gradient descent (SGD) in an asynchronous manner can be viewed as adding a momentum-like term to the SGD iteration. Our result does not assume convexity of the objective function, so it is applicable to deep learning systems. We observe that a standard queuing model of asynchrony results in a form of momentum that is commonly used by deep learning practitioners. This forges a link between queuing theory and asynchrony in deep learning systems, which could be useful for systems builders. For convolutional neural networks, we experimentally validate that the degree of asynchrony directly correlates with the momentum, confirming our main result. An important implication is that tuning the momentum parameter is important when considering different levels of asynchrony. We assert that properly tuned momentum reduces the number of steps required for convergence. Finally, our theory suggests new ways of counteracting the adverse effects of asynchrony: a simple mechanism like using negative algorithmic momentum can improve performance under high asynchrony. Since asynchronous methods have better hardware efficiency, this result may shed light on when asynchronous execution is more efficient for deep learning systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge