Asynchronous Stochastic Gradient MCMC with Elastic Coupling
Paper and Code
Dec 08, 2016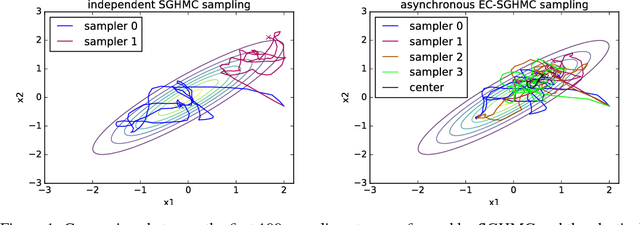
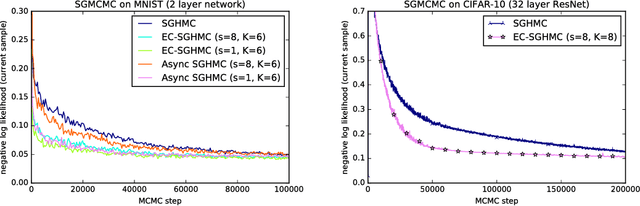
We consider parallel asynchronous Markov Chain Monte Carlo (MCMC) sampling for problems where we can leverage (stochastic) gradients to define continuous dynamics which explore the target distribution. We outline a solution strategy for this setting based on stochastic gradient Hamiltonian Monte Carlo sampling (SGHMC) which we alter to include an elastic coupling term that ties together multiple MCMC instances. The proposed strategy turns inherently sequential HMC algorithms into asynchronous parallel versions. First experiments empirically show that the resulting parallel sampler significantly speeds up exploration of the target distribution, when compared to standard SGHMC, and is less prone to the harmful effects of stale gradients than a naive parallelization approach.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge