Are Powerful Graph Neural Nets Necessary? A Dissection on Graph Classification
Paper and Code
May 24, 2019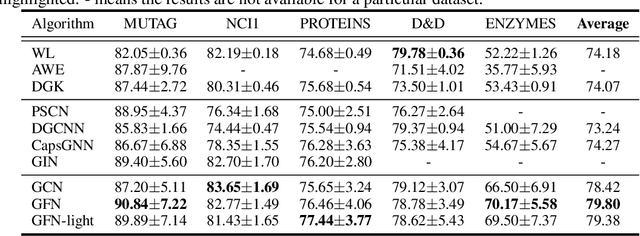
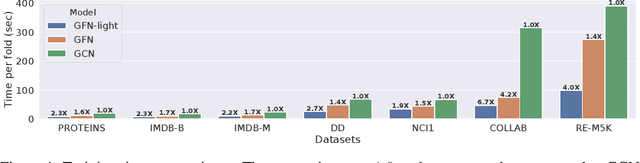
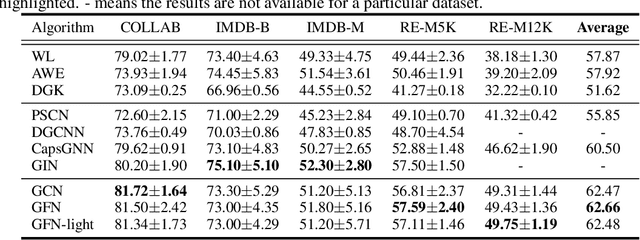
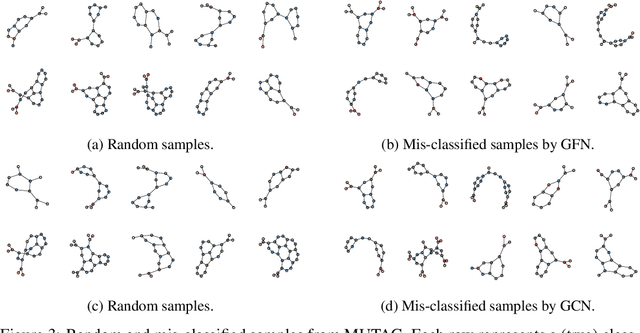
Graph Neural Nets (GNNs) have received increasing attentions, partially due to their superior performance in many node and graph classification tasks. However, there is a lack of understanding on what they are learning and how sophisticated the learned graph functions are. In this work, we first propose Graph Feature Network (GFN), a simple lightweight neural net defined on a set of graph augmented features. We then propose a dissection of GNNs on graph classification into two parts: 1) the graph filtering, where graph-based neighbor aggregations are performed, and 2) the set function, where a set of hidden node features are composed for prediction. We prove that GFN can be derived by linearizing graph filtering part of GNNs, and leverage it to test the importance of the two parts separately. Empirically we perform evaluations on common graph classification benchmarks. To our surprise, we find that, despite the simplification, GFN could match or exceed the best accuracies produced by recently proposed GNNs, with a fraction of computation cost. Our results suggest that linear graph filtering with non-linear set function is powerful enough, and common graph classification benchmarks seem inadequate for testing advanced GNN variants.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge