Annealed Langevin Dynamics for Massive MIMO Detection
Paper and Code
May 11, 2022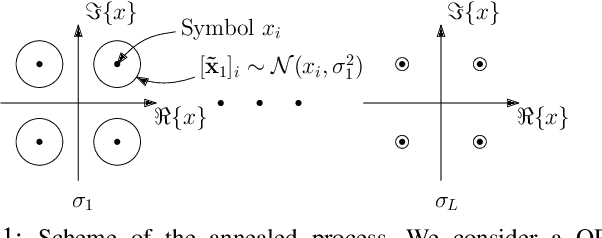
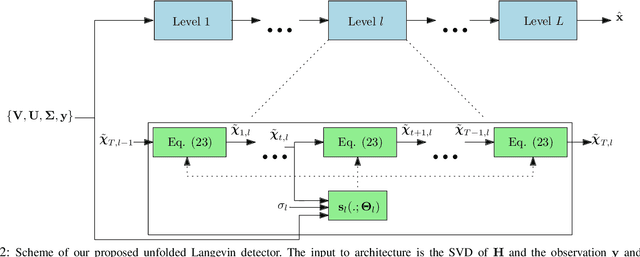
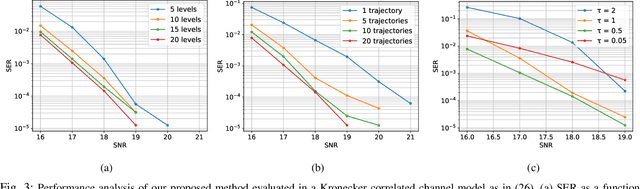
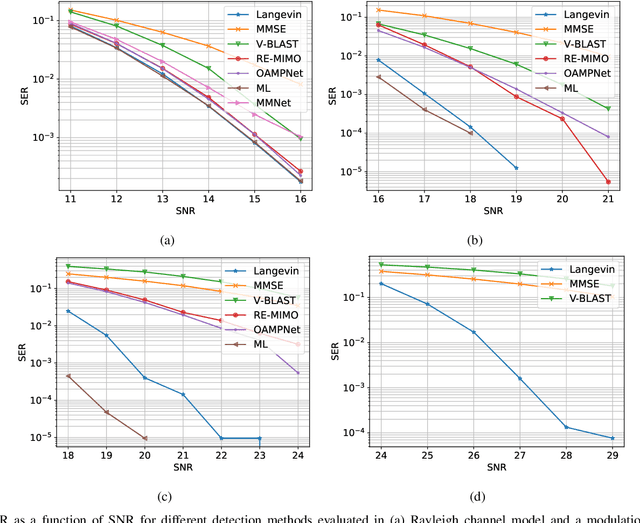
Solving the optimal symbol detection problem in multiple-input multiple-output (MIMO) systems is known to be NP-hard. Hence, the objective of any detector of practical relevance is to get reasonably close to the optimal solution while keeping the computational complexity in check. In this work, we propose a MIMO detector based on an annealed version of Langevin (stochastic) dynamics. More precisely, we define a stochastic dynamical process whose stationary distribution coincides with the posterior distribution of the symbols given our observations. In essence, this allows us to approximate the maximum a posteriori estimator of the transmitted symbols by sampling from the proposed Langevin dynamic. Furthermore, we carefully craft this stochastic dynamic by gradually adding a sequence of noise with decreasing variance to the trajectories, which ensures that the estimated symbols belong to a pre-specified discrete constellation. Based on the proposed MIMO detector, we also design a robust version of the method by unfolding and parameterizing one term -- the score of the likelihood -- by a neural network. Through numerical experiments in both synthetic and real-world data, we show that our proposed detector yields state-of-the-art symbol error rate performance and the robust version becomes noise-variance agnostic.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge