Anchor-Changing Regularized Natural Policy Gradient for Multi-Objective Reinforcement Learning
Paper and Code
Jun 10, 2022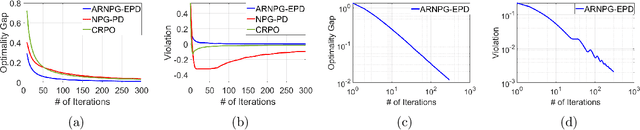



We study policy optimization for Markov decision processes (MDPs) with multiple reward value functions, which are to be jointly optimized according to given criteria such as proportional fairness (smooth concave scalarization), hard constraints (constrained MDP), and max-min trade-off. We propose an Anchor-changing Regularized Natural Policy Gradient (ARNPG) framework, which can systematically incorporate ideas from well-performing first-order methods into the design of policy optimization algorithms for multi-objective MDP problems. Theoretically, the designed algorithms based on the ARNPG framework achieve $\tilde{O}(1/T)$ global convergence with exact gradients. Empirically, the ARNPG-guided algorithms also demonstrate superior performance compared to some existing policy gradient-based approaches in both exact gradients and sample-based scenarios.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge