Analyzing the Robustness of Nearest Neighbors to Adversarial Examples
Paper and Code
Jul 15, 2018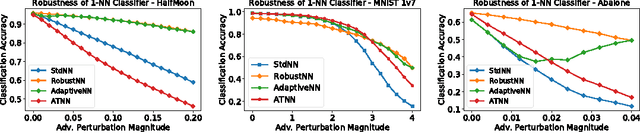

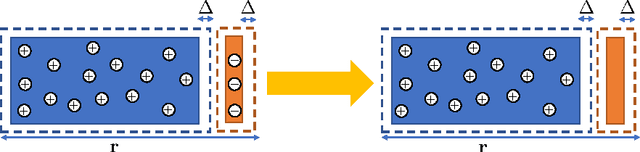

Motivated by safety-critical applications, test-time attacks on classifiers via adversarial examples has recently received a great deal of attention. However, there is a general lack of understanding on why adversarial examples arise; whether they originate due to inherent properties of data or due to lack of training samples remains ill-understood. In this work, we introduce a theoretical framework analogous to bias-variance theory for understanding these effects. We use our framework to analyze the robustness of a canonical non-parametric classifier - the k-nearest neighbors. Our analysis shows that its robustness properties depend critically on the value of k - the classifier may be inherently non-robust for small k, but its robustness approaches that of the Bayes Optimal classifier for fast-growing k. We propose a novel modified 1-nearest neighbor classifier, and guarantee its robustness in the large sample limit. Our experiments suggest that this classifier may have good robustness properties even for reasonable data set sizes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge