Analysis of Fast Structured Dictionary Learning

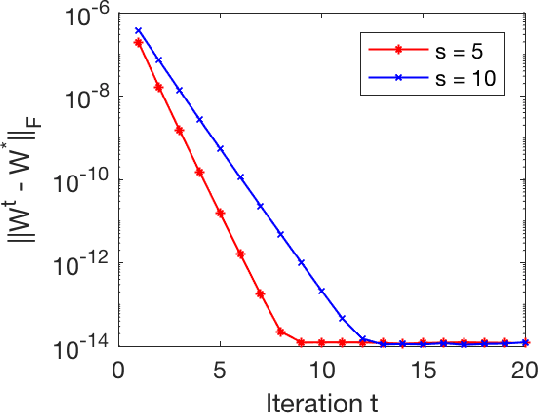
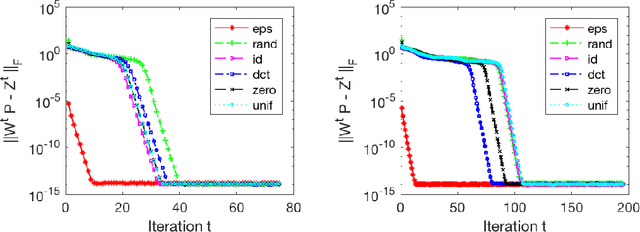
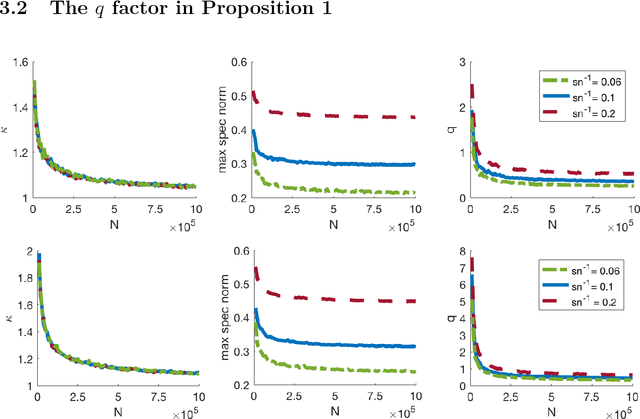
Sparsity-based models and techniques have been exploited in many signal processing and imaging applications. Data-driven methods based on dictionary and transform learning enable learning rich image features from data, and can outperform analytical models. In particular, alternating optimization algorithms for dictionary learning have been popular. In this work, we focus on alternating minimization for a specific structured unitary operator learning problem, and provide a convergence analysis. While the algorithm converges to the critical points of the problem generally, our analysis establishes under mild assumptions, the local linear convergence of the algorithm to the underlying generating model of the data. Analysis and numerical simulations show that our assumptions hold well for standard probabilistic data models. In practice, the algorithm is robust to initialization.