Analog Sparse Approximation with Applications to Compressed Sensing
Paper and Code
Nov 17, 2011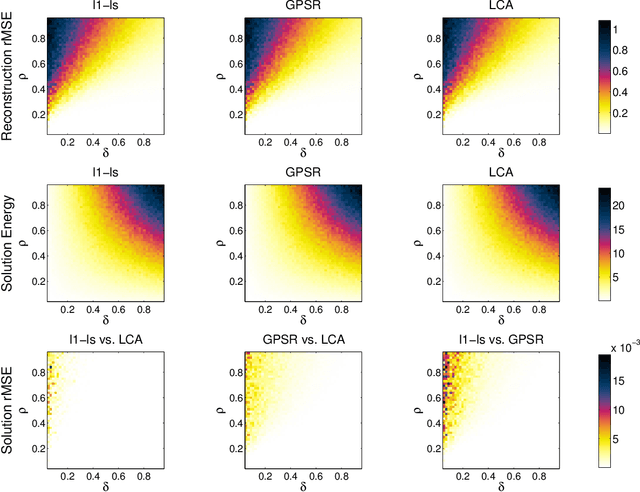
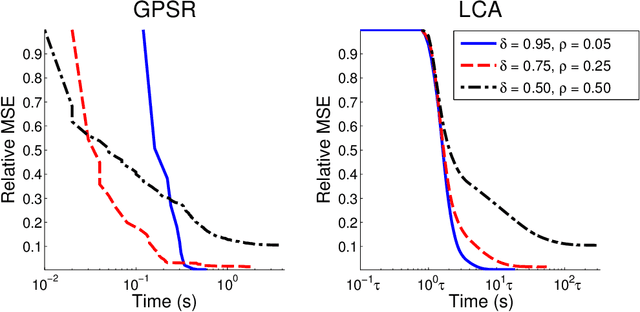
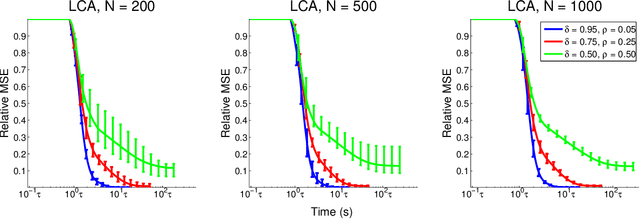
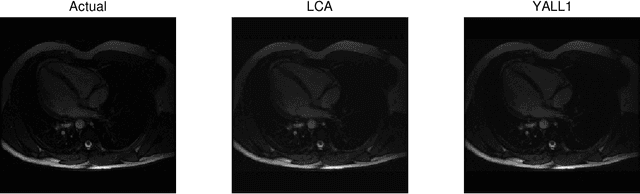
Recent research has shown that performance in signal processing tasks can often be significantly improved by using signal models based on sparse representations, where a signal is approximated using a small number of elements from a fixed dictionary. Unfortunately, inference in this model involves solving non-smooth optimization problems that are computationally expensive. While significant efforts have focused on developing digital algorithms specifically for this problem, these algorithms are inappropriate for many applications because of the time and power requirements necessary to solve large optimization problems. Based on recent work in computational neuroscience, we explore the potential advantages of continuous time dynamical systems for solving sparse approximation problems if they were implemented in analog VLSI. Specifically, in the simulated task of recovering synthetic and MRI data acquired via compressive sensing techniques, we show that these systems can potentially perform recovery at time scales of 10-20{\mu}s, supporting datarates of 50-100 kHz (orders of magnitude faster that digital algorithms). Furthermore, we show analytically that a wide range of sparse approximation problems can be solved in the same basic architecture, including approximate $\ell^p$ norms, modified $\ell^1$ norms, re-weighted $\ell^1$ and $\ell^2$, the block $\ell^1$ norm and classic Tikhonov regularization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge