An Investigation of the Bias-Variance Tradeoff in Meta-Gradients
Paper and Code
Sep 22, 2022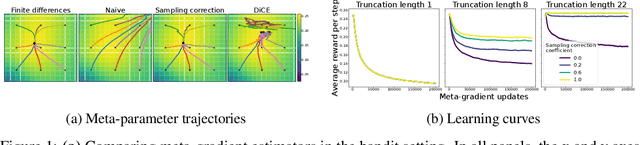



Meta-gradients provide a general approach for optimizing the meta-parameters of reinforcement learning (RL) algorithms. Estimation of meta-gradients is central to the performance of these meta-algorithms, and has been studied in the setting of MAML-style short-horizon meta-RL problems. In this context, prior work has investigated the estimation of the Hessian of the RL objective, as well as tackling the problem of credit assignment to pre-adaptation behavior by making a sampling correction. However, we show that Hessian estimation, implemented for example by DiCE and its variants, always adds bias and can also add variance to meta-gradient estimation. Meanwhile, meta-gradient estimation has been studied less in the important long-horizon setting, where backpropagation through the full inner optimization trajectories is not feasible. We study the bias and variance tradeoff arising from truncated backpropagation and sampling correction, and additionally compare to evolution strategies, which is a recently popular alternative strategy to long-horizon meta-learning. While prior work implicitly chooses points in this bias-variance space, we disentangle the sources of bias and variance and present an empirical study that relates existing estimators to each other.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge