An Index Policy Based on Sarsa and Q-learning for Heterogeneous Smart Target Tracking
Paper and Code
Feb 19, 2024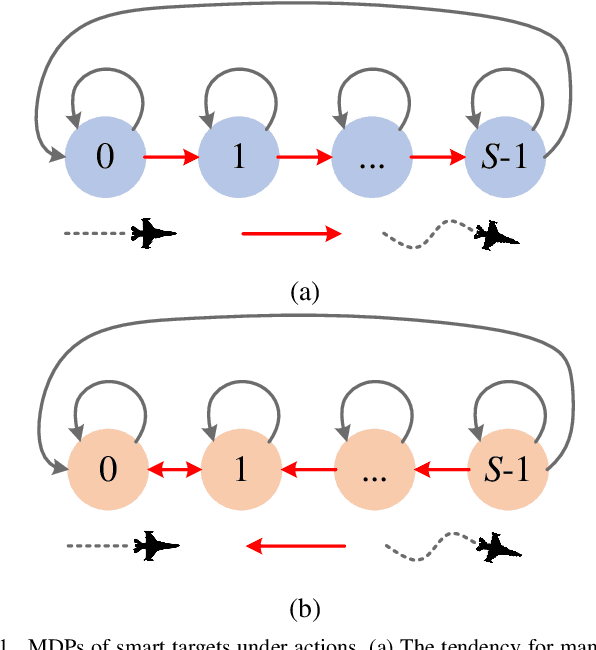
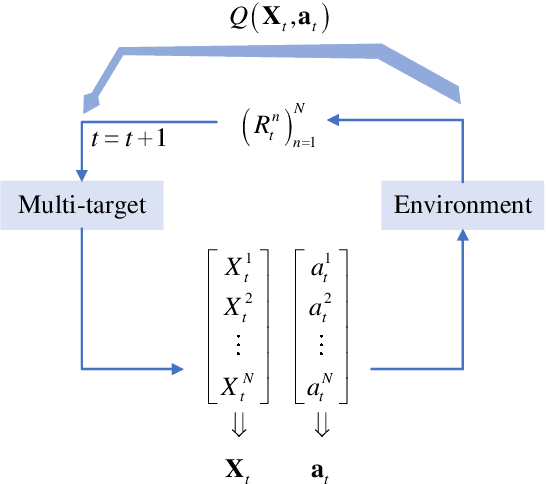
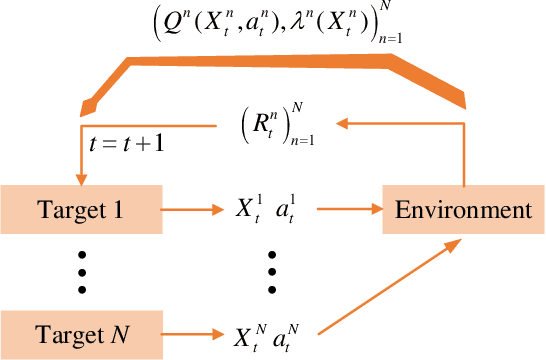
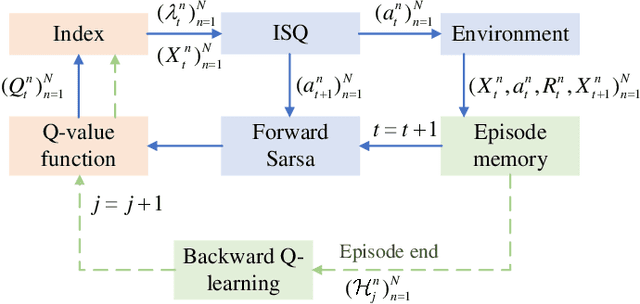
In solving the non-myopic radar scheduling for multiple smart target tracking within an active and passive radar network, we need to consider both short-term enhanced tracking performance and a higher probability of target maneuvering in the future with active tracking. Acquiring the long-term tracking performance while scheduling the beam resources of active and passive radars poses a challenge. To address this challenge, we model this problem as a Markov decision process consisting of parallel restless bandit processes. Each bandit process is associated with a smart target, of which the estimation state evolves according to different discrete dynamic models for different actions - whether or not the target is being tracked. The discrete state is defined by the dynamic mode. The problem exhibits the curse of dimensionality, where optimal solutions are in general intractable. We resort to heuristics through the famous restless multi-armed bandit techniques. It follows with efficient scheduling policies based on the indices that are real numbers representing the marginal rewards of taking different actions. For the inevitable practical case with unknown transition matrices, we propose a new method that utilizes the forward Sarsa and backward Q-learning to approximate the indices through adapting the state-action value functions, or equivalently the Q-functions, and propose a new policy, namely ISQ, aiming to maximize the long-term tracking rewards. Numerical results demonstrate that the proposed ISQ policy outperforms conventional Q-learning-based methods and rapidly converges to the well-known Whittle index policy with revealed state transition models, which is considered the benchmark.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge