An empirical analysis of dropout in piecewise linear networks
Paper and Code
Jan 02, 2014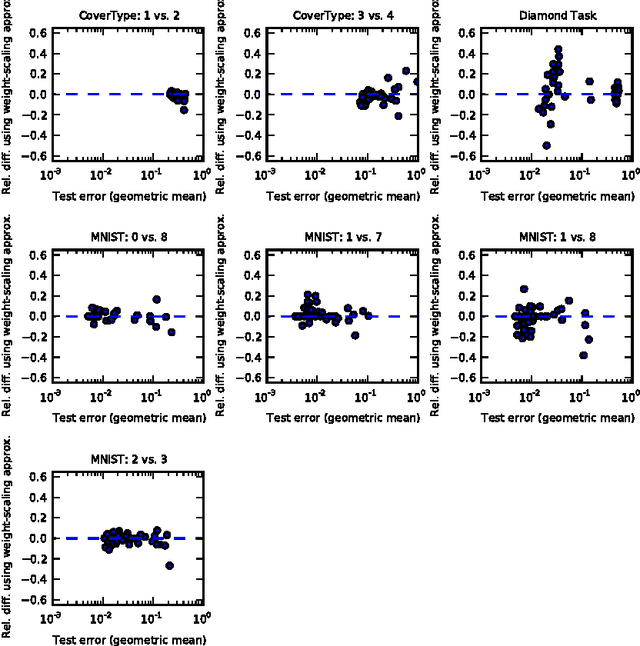
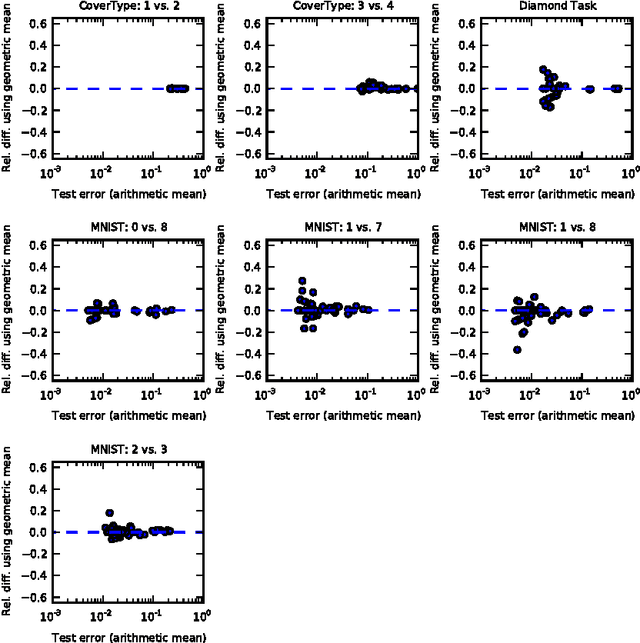
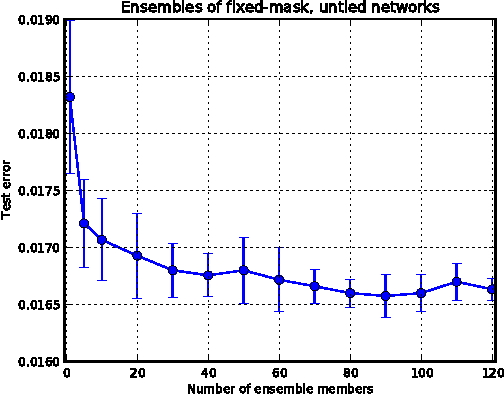
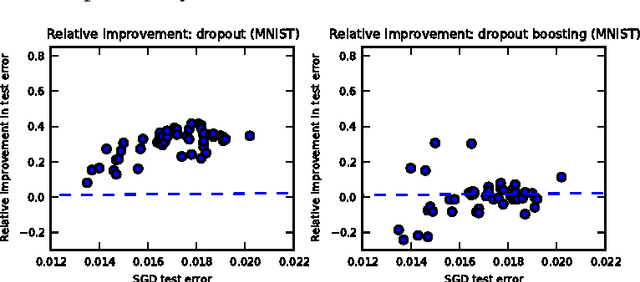
The recently introduced dropout training criterion for neural networks has been the subject of much attention due to its simplicity and remarkable effectiveness as a regularizer, as well as its interpretation as a training procedure for an exponentially large ensemble of networks that share parameters. In this work we empirically investigate several questions related to the efficacy of dropout, specifically as it concerns networks employing the popular rectified linear activation function. We investigate the quality of the test time weight-scaling inference procedure by evaluating the geometric average exactly in small models, as well as compare the performance of the geometric mean to the arithmetic mean more commonly employed by ensemble techniques. We explore the effect of tied weights on the ensemble interpretation by training ensembles of masked networks without tied weights. Finally, we investigate an alternative criterion based on a biased estimator of the maximum likelihood ensemble gradient.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge