An efficient K -means clustering algorithm for massive data
Paper and Code
Jan 09, 2018

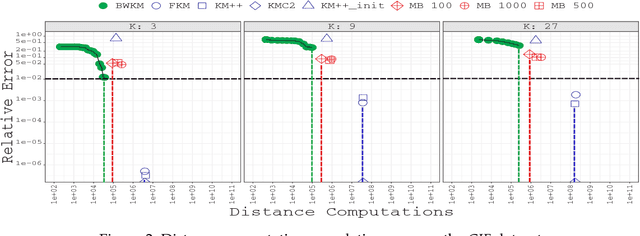

The analysis of continously larger datasets is a task of major importance in a wide variety of scientific fields. In this sense, cluster analysis algorithms are a key element of exploratory data analysis, due to their easiness in the implementation and relatively low computational cost. Among these algorithms, the K -means algorithm stands out as the most popular approach, besides its high dependency on the initial conditions, as well as to the fact that it might not scale well on massive datasets. In this article, we propose a recursive and parallel approximation to the K -means algorithm that scales well on both the number of instances and dimensionality of the problem, without affecting the quality of the approximation. In order to achieve this, instead of analyzing the entire dataset, we work on small weighted sets of points that mostly intend to extract information from those regions where it is harder to determine the correct cluster assignment of the original instances. In addition to different theoretical properties, which deduce the reasoning behind the algorithm, experimental results indicate that our method outperforms the state-of-the-art in terms of the trade-off between number of distance computations and the quality of the solution obtained.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge