An Efficient Dual Approach to Distance Metric Learning

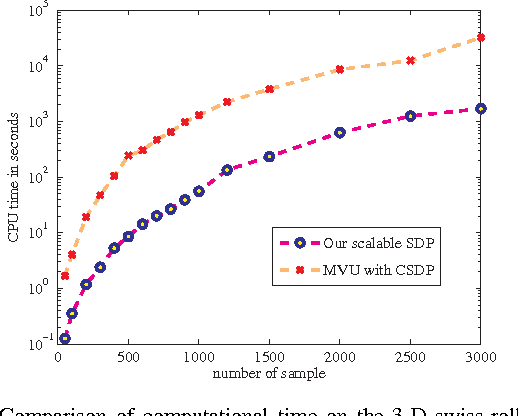
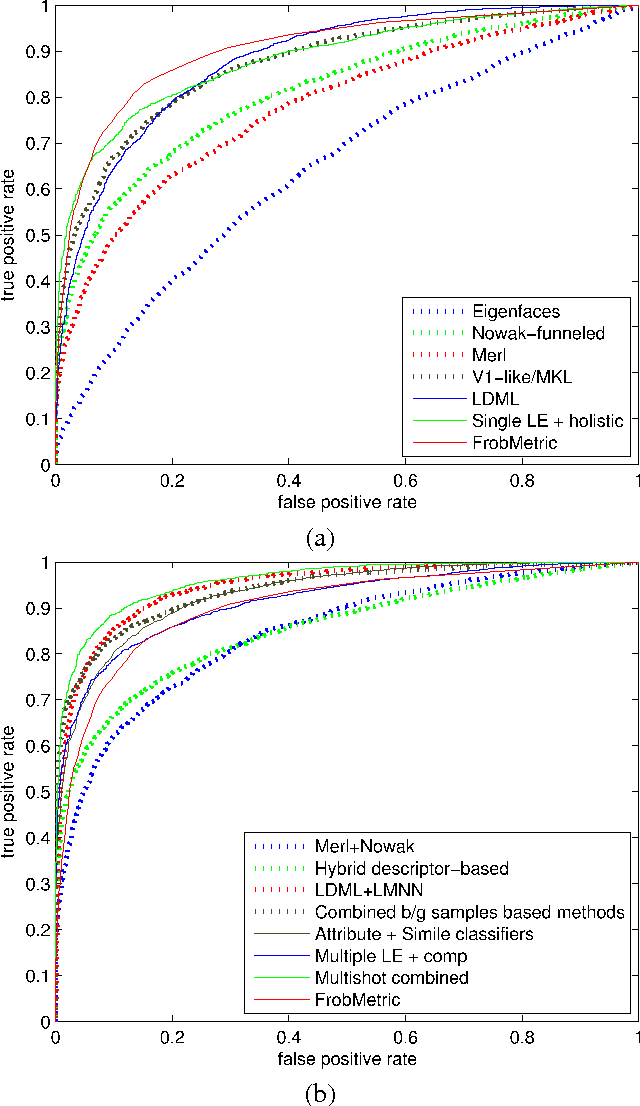
Distance metric learning is of fundamental interest in machine learning because the distance metric employed can significantly affect the performance of many learning methods. Quadratic Mahalanobis metric learning is a popular approach to the problem, but typically requires solving a semidefinite programming (SDP) problem, which is computationally expensive. Standard interior-point SDP solvers typically have a complexity of $O(D^{6.5})$ (with $D$ the dimension of input data), and can thus only practically solve problems exhibiting less than a few thousand variables. Since the number of variables is $D (D+1) / 2 $, this implies a limit upon the size of problem that can practically be solved of around a few hundred dimensions. The complexity of the popular quadratic Mahalanobis metric learning approach thus limits the size of problem to which metric learning can be applied. Here we propose a significantly more efficient approach to the metric learning problem based on the Lagrange dual formulation of the problem. The proposed formulation is much simpler to implement, and therefore allows much larger Mahalanobis metric learning problems to be solved. The time complexity of the proposed method is $O (D ^ 3) $, which is significantly lower than that of the SDP approach. Experiments on a variety of datasets demonstrate that the proposed method achieves an accuracy comparable to the state-of-the-art, but is applicable to significantly larger problems. We also show that the proposed method can be applied to solve more general Frobenius-norm regularized SDP problems approximately.