An additive graphical model for discrete data
Paper and Code
Dec 29, 2021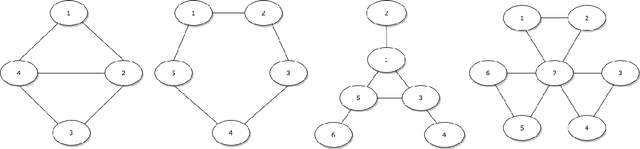
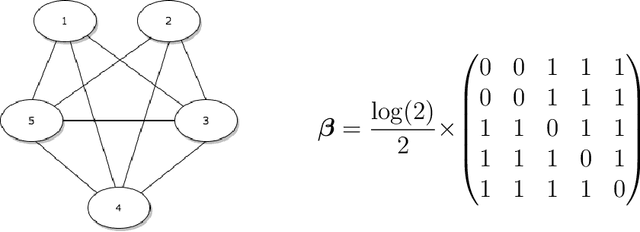
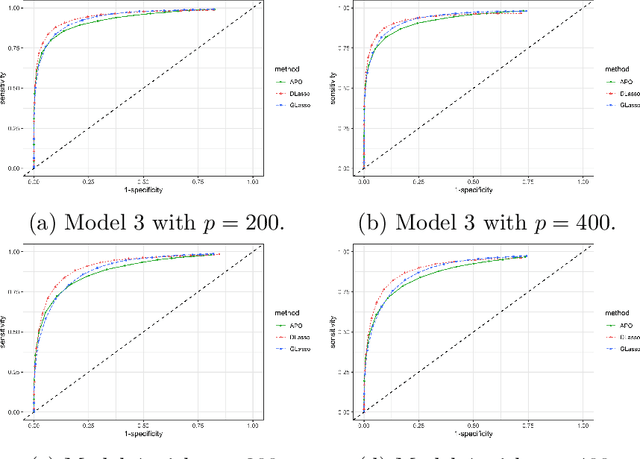
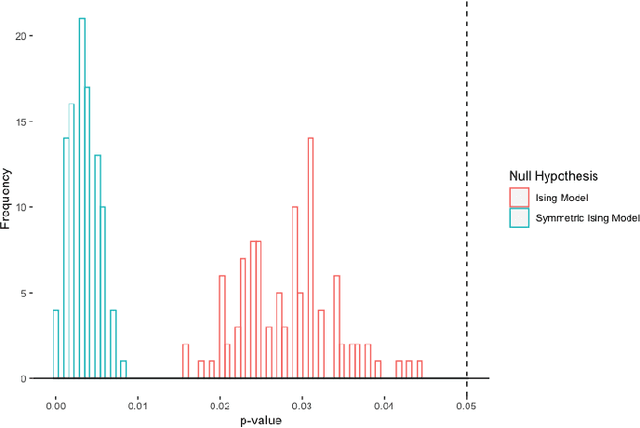
We introduce a nonparametric graphical model for discrete node variables based on additive conditional independence. Additive conditional independence is a three way statistical relation that shares similar properties with conditional independence by satisfying the semi-graphoid axioms. Based on this relation we build an additive graphical model for discrete variables that does not suffer from the restriction of a parametric model such as the Ising model. We develop an estimator of the new graphical model via the penalized estimation of the discrete version of the additive precision operator and establish the consistency of the estimator under the ultrahigh-dimensional setting. Along with these methodological developments, we also exploit the properties of discrete random variables to uncover a deeper relation between additive conditional independence and conditional independence than previously known. The new graphical model reduces to a conditional independence graphical model under certain sparsity conditions. We conduct simulation experiments and analysis of an HIV antiretroviral therapy data set to compare the new method with existing ones.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge