AMRA*: Anytime Multi-Resolution Multi-Heuristic A*
Paper and Code
Oct 11, 2021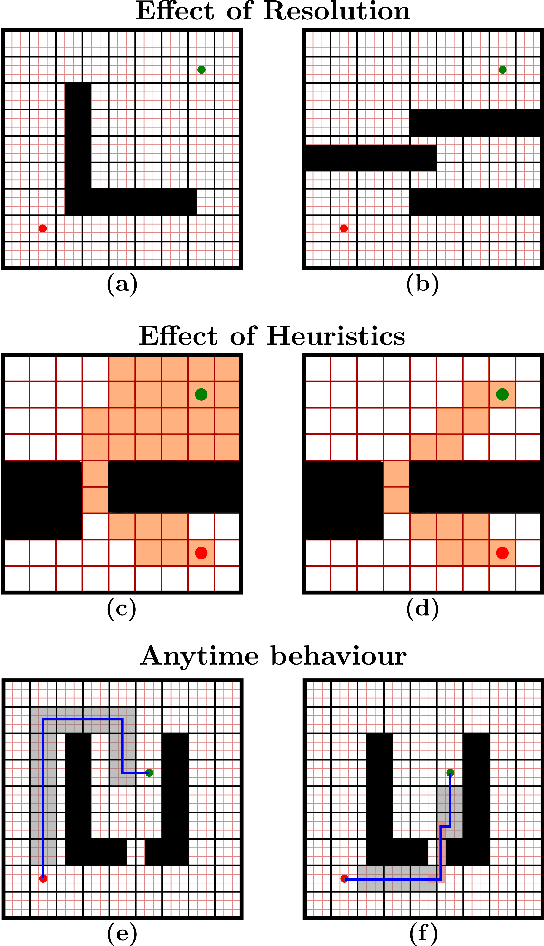
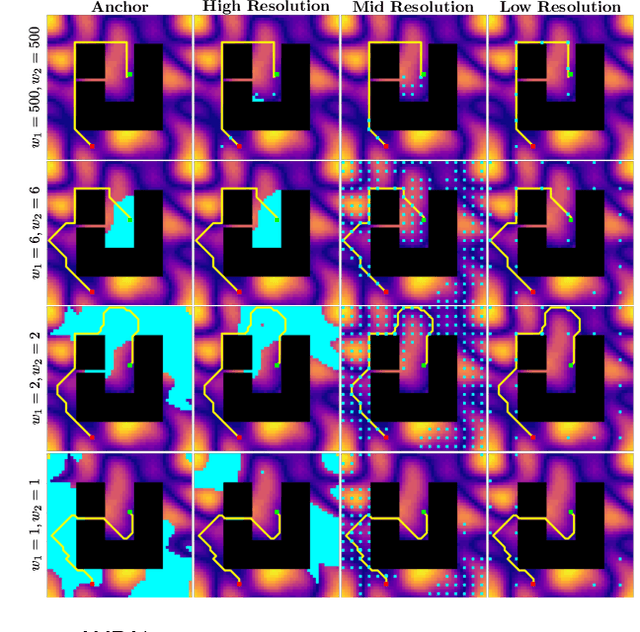

Heuristic search-based motion planning algorithms typically discretise the search space in order to solve the shortest path problem. Their performance is closely related to this discretisation. A fine discretisation allows for better approximations of the continuous search space, but makes the search for a solution more computationally costly. A coarser resolution might allow the algorithms to find solutions quickly at the expense of quality. For large state spaces, it can be beneficial to search for solutions across multiple resolutions even though defining the discretisations is challenging. The recently proposed algorithm Multi-Resolution A* (MRA*) searches over multiple resolutions. It traverses large areas of obstacle-free space and escapes local minima at a coarse resolution. It can also navigate so-called narrow passageways at a finer resolution. In this work, we develop AMRA*, an anytime version of MRA*. AMRA* tries to find a solution quickly using the coarse resolution as much as possible. It then refines the solution by relying on the fine resolution to discover better paths that may not have been available at the coarse resolution. In addition to being anytime, AMRA* can also leverage information sharing between multiple heuristics. We prove that AMRA* is complete and optimal (in-the-limit of time) with respect to the finest resolution. We show its performance on 2D grid navigation and 4D kinodynamic planning problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge