Almost Boltzmann Exploration
Paper and Code
Jan 25, 2019
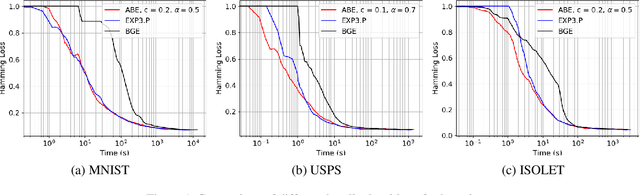
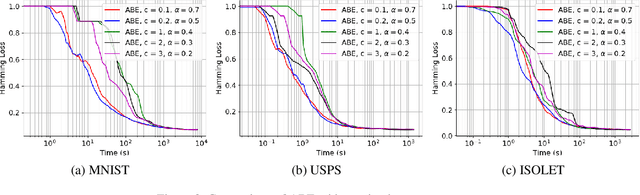
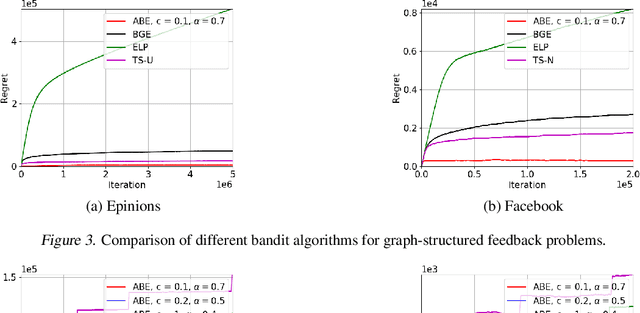
Boltzmann exploration is widely used in reinforcement learning to provide a trade-off between exploration and exploitation. Recently, in (Cesa-Bianchi et al., 2017) it has been shown that pure Boltzmann exploration does not perform well from a regret perspective, even in the simplest setting of stochastic multi-armed bandit (MAB) problems. In this paper, we show that a simple modification to Boltzmann exploration, motivated by a variation of the standard doubling trick, achieves $O(K\log^{1+\alpha} T)$ regret for a stochastic MAB problem with $K$ arms, where $\alpha>0$ is a parameter of the algorithm. This improves on the result in (Cesa-Bianchi et al., 2017), where an algorithm inspired by the Gumbel-softmax trick achieves $O(K\log^2 T)$ regret. We also show that our algorithm achieves $O(\beta(G) \log^{1+\alpha} T)$ regret in stochastic MAB problems with graph-structured feedback, without knowledge of the graph structure, where $\beta(G)$ is the independence number of the feedback graph. Additionally, we present extensive experimental results on real datasets and applications for multi-armed bandits with both traditional bandit feedback and graph-structured feedback. In all cases, our algorithm performs as well or better than the state-of-the-art.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge