AI Poincaré 2.0: Machine Learning Conservation Laws from Differential Equations
Paper and Code
Mar 23, 2022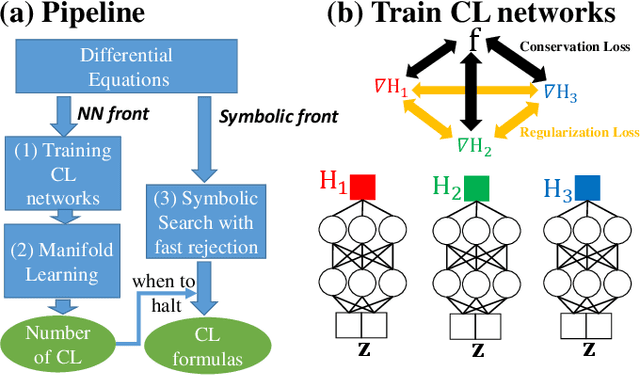
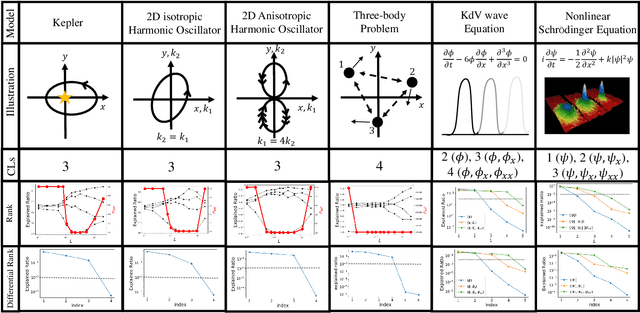
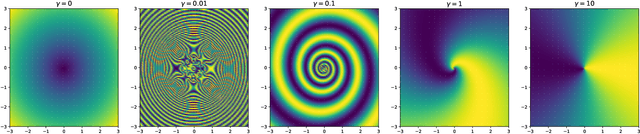
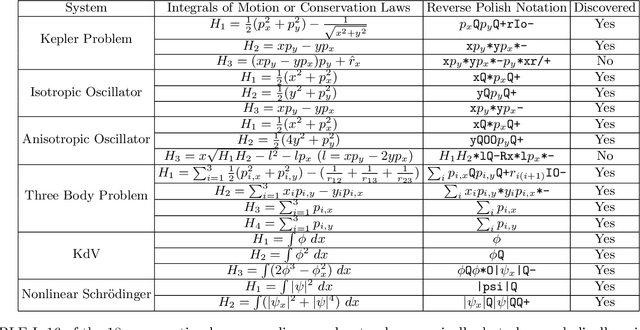
We present a machine learning algorithm that discovers conservation laws from differential equations, both numerically (parametrized as neural networks) and symbolically, ensuring their functional independence (a non-linear generalization of linear independence). Our independence module can be viewed as a nonlinear generalization of singular value decomposition. Our method can readily handle inductive biases for conservation laws. We validate it with examples including the 3-body problem, the KdV equation and nonlinear Schr\"odinger equation.
* 17 pages, 10 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge