Aggregated Wasserstein Metric and State Registration for Hidden Markov Models

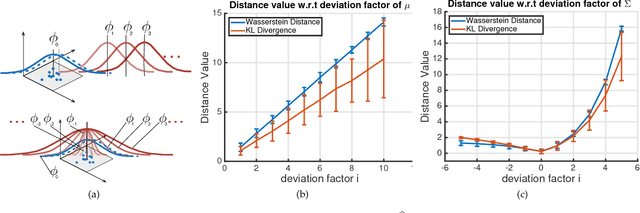
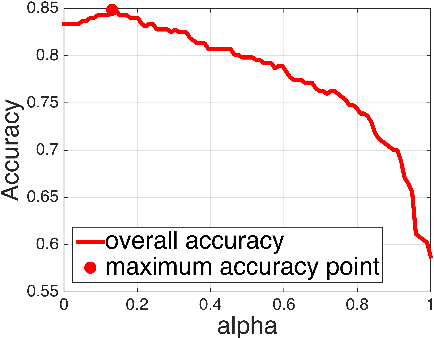
We propose a framework, named Aggregated Wasserstein, for computing a dissimilarity measure or distance between two Hidden Markov Models with state conditional distributions being Gaussian. For such HMMs, the marginal distribution at any time position follows a Gaussian mixture distribution, a fact exploited to softly match, aka register, the states in two HMMs. We refer to such HMMs as Gaussian mixture model-HMM (GMM-HMM). The registration of states is inspired by the intrinsic relationship of optimal transport and the Wasserstein metric between distributions. Specifically, the components of the marginal GMMs are matched by solving an optimal transport problem where the cost between components is the Wasserstein metric for Gaussian distributions. The solution of the optimization problem is a fast approximation to the Wasserstein metric between two GMMs. The new Aggregated Wasserstein distance is a semi-metric and can be computed without generating Monte Carlo samples. It is invariant to relabeling or permutation of states. The distance is defined meaningfully even for two HMMs that are estimated from data of different dimensionality, a situation that can arise due to missing variables. This distance quantifies the dissimilarity of GMM-HMMs by measuring both the difference between the two marginal GMMs and that between the two transition matrices. Our new distance is tested on tasks of retrieval, classification, and t-SNE visualization of time series. Experiments on both synthetic and real data have demonstrated its advantages in terms of accuracy as well as efficiency in comparison with existing distances based on the Kullback-Leibler divergence.