Adversarial Margin Maximization Networks
Paper and Code
Nov 14, 2019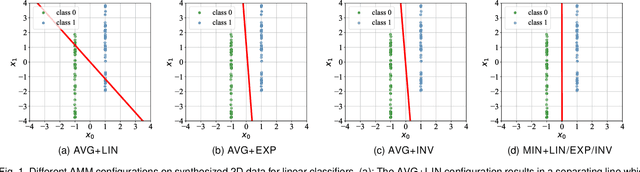

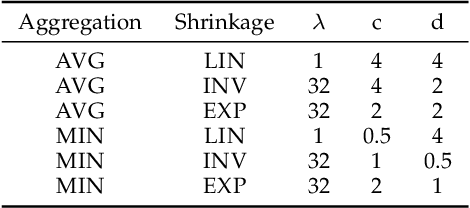
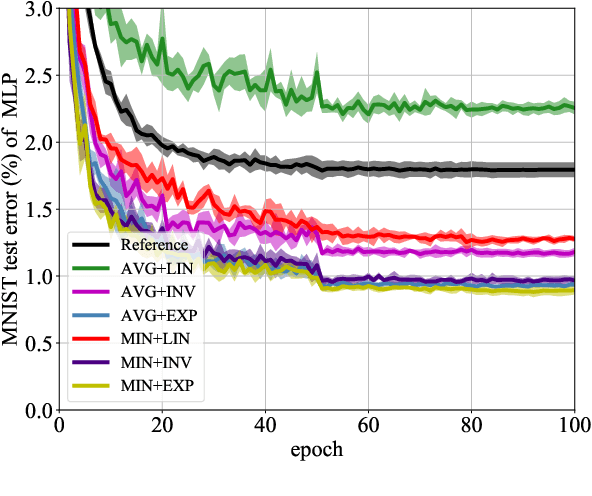
The tremendous recent success of deep neural networks (DNNs) has sparked a surge of interest in understanding their predictive ability. Unlike the human visual system which is able to generalize robustly and learn with little supervision, DNNs normally require a massive amount of data to learn new concepts. In addition, research works also show that DNNs are vulnerable to adversarial examples-maliciously generated images which seem perceptually similar to the natural ones but are actually formed to fool learning models, which means the models have problem generalizing to unseen data with certain type of distortions. In this paper, we analyze the generalization ability of DNNs comprehensively and attempt to improve it from a geometric point of view. We propose adversarial margin maximization (AMM), a learning-based regularization which exploits an adversarial perturbation as a proxy. It encourages a large margin in the input space, just like the support vector machines. With a differentiable formulation of the perturbation, we train the regularized DNNs simply through back-propagation in an end-to-end manner. Experimental results on various datasets (including MNIST, CIFAR-10/100, SVHN and ImageNet) and different DNN architectures demonstrate the superiority of our method over previous state-of-the-arts. Code and models for reproducing our results will be made publicly available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge