Adversarial Learning for Neural PDE Solvers with Sparse Data
Paper and Code
Sep 04, 2024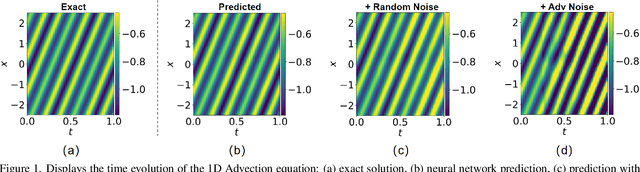
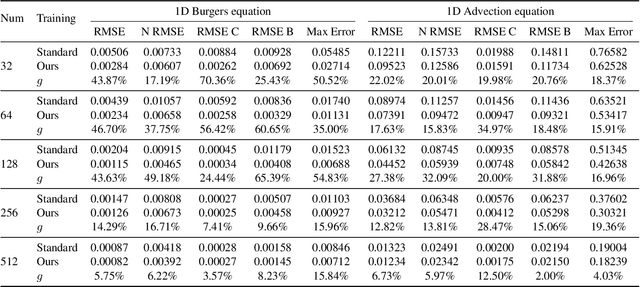
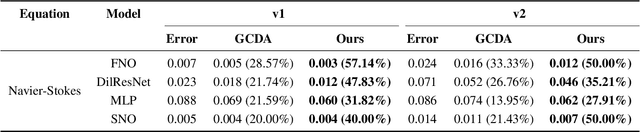
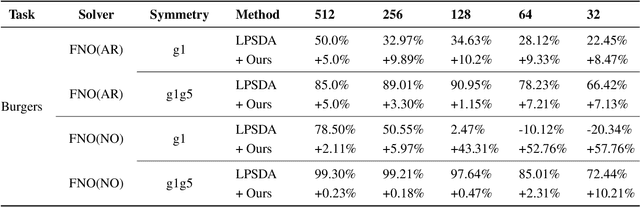
Neural network solvers for partial differential equations (PDEs) have made significant progress, yet they continue to face challenges related to data scarcity and model robustness. Traditional data augmentation methods, which leverage symmetry or invariance, impose strong assumptions on physical systems that often do not hold in dynamic and complex real-world applications. To address this research gap, this study introduces a universal learning strategy for neural network PDEs, named Systematic Model Augmentation for Robust Training (SMART). By focusing on challenging and improving the model's weaknesses, SMART reduces generalization error during training under data-scarce conditions, leading to significant improvements in prediction accuracy across various PDE scenarios. The effectiveness of the proposed method is demonstrated through both theoretical analysis and extensive experimentation. The code will be available.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge