Advancing Bayesian Optimization via Learning Correlated Latent Space
Paper and Code
Nov 20, 2023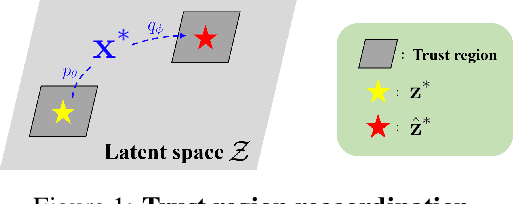

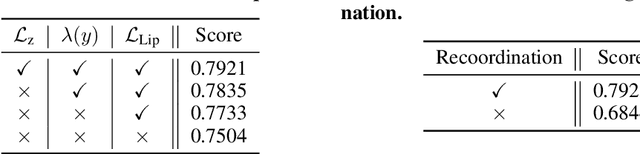
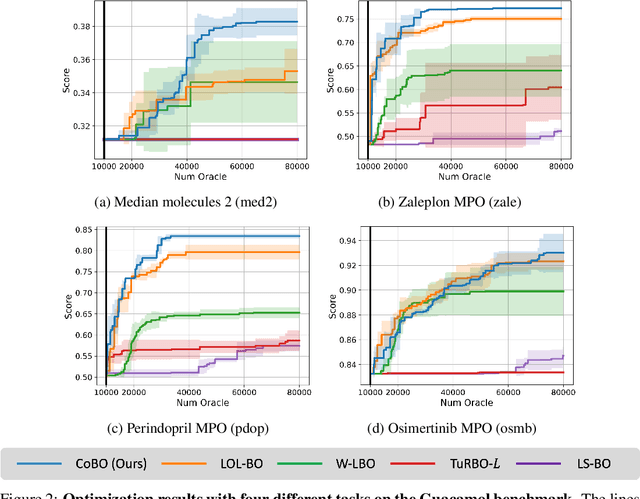
Bayesian optimization is a powerful method for optimizing black-box functions with limited function evaluations. Recent works have shown that optimization in a latent space through deep generative models such as variational autoencoders leads to effective and efficient Bayesian optimization for structured or discrete data. However, as the optimization does not take place in the input space, it leads to an inherent gap that results in potentially suboptimal solutions. To alleviate the discrepancy, we propose Correlated latent space Bayesian Optimization (CoBO), which focuses on learning correlated latent spaces characterized by a strong correlation between the distances in the latent space and the distances within the objective function. Specifically, our method introduces Lipschitz regularization, loss weighting, and trust region recoordination to minimize the inherent gap around the promising areas. We demonstrate the effectiveness of our approach on several optimization tasks in discrete data, such as molecule design and arithmetic expression fitting, and achieve high performance within a small budget.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge