Advances in Variational Inference
Paper and Code
Oct 23, 2018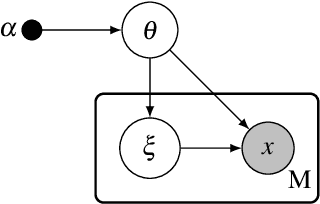

Many modern unsupervised or semi-supervised machine learning algorithms rely on Bayesian probabilistic models. These models are usually intractable and thus require approximate inference. Variational inference (VI) lets us approximate a high-dimensional Bayesian posterior with a simpler variational distribution by solving an optimization problem. This approach has been successfully used in various models and large-scale applications. In this review, we give an overview of recent trends in variational inference. We first introduce standard mean field variational inference, then review recent advances focusing on the following aspects: (a) scalable VI, which includes stochastic approximations, (b) generic VI, which extends the applicability of VI to a large class of otherwise intractable models, such as non-conjugate models, (c) accurate VI, which includes variational models beyond the mean field approximation or with atypical divergences, and (d) amortized VI, which implements the inference over local latent variables with inference networks. Finally, we provide a summary of promising future research directions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge