AdaTrans: Feature-wise and Sample-wise Adaptive Transfer Learning for High-dimensional Regression
Paper and Code
Mar 20, 2024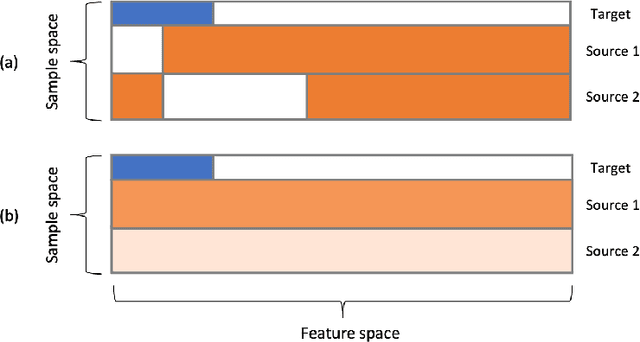
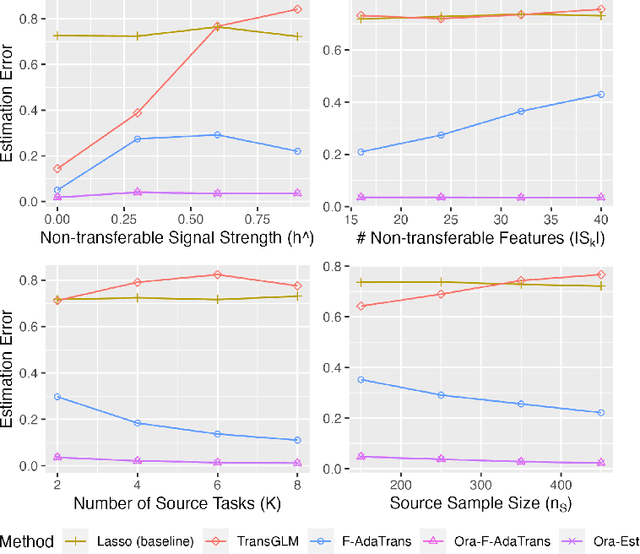
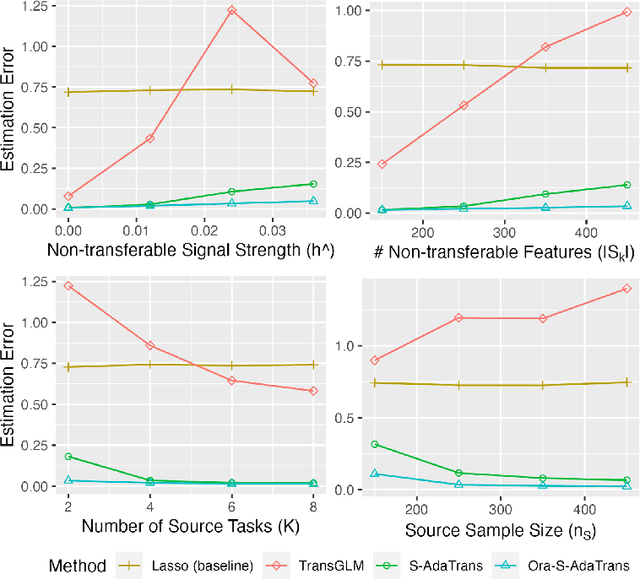
We consider the transfer learning problem in the high dimensional setting, where the feature dimension is larger than the sample size. To learn transferable information, which may vary across features or the source samples, we propose an adaptive transfer learning method that can detect and aggregate the feature-wise (F-AdaTrans) or sample-wise (S-AdaTrans) transferable structures. We achieve this by employing a novel fused-penalty, coupled with weights that can adapt according to the transferable structure. To choose the weight, we propose a theoretically informed, data-driven procedure, enabling F-AdaTrans to selectively fuse the transferable signals with the target while filtering out non-transferable signals, and S-AdaTrans to obtain the optimal combination of information transferred from each source sample. The non-asymptotic rates are established, which recover existing near-minimax optimal rates in special cases. The effectiveness of the proposed method is validated using both synthetic and real data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge