Adaptive Graph-based Generalized Regression Model for Unsupervised Feature Selection
Paper and Code
Dec 27, 2020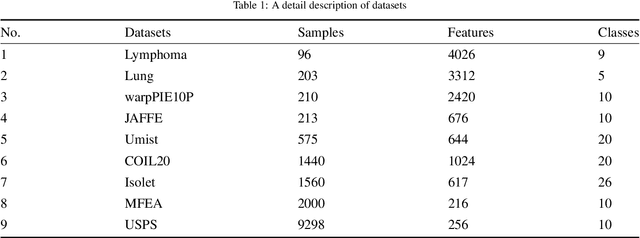
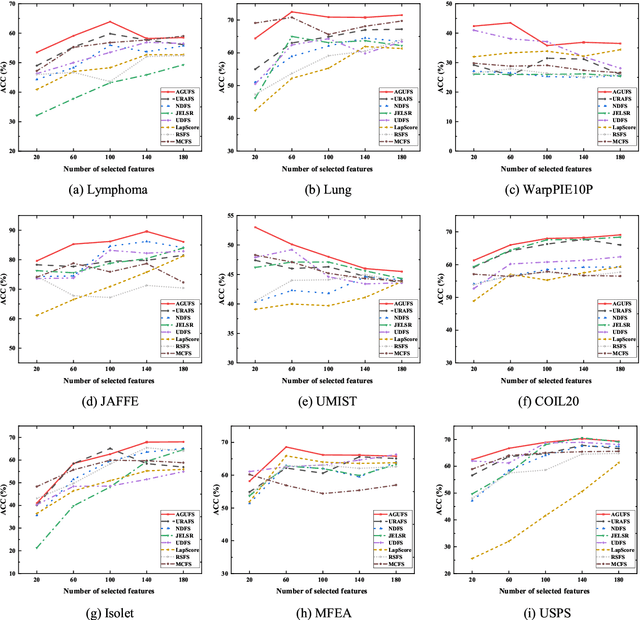
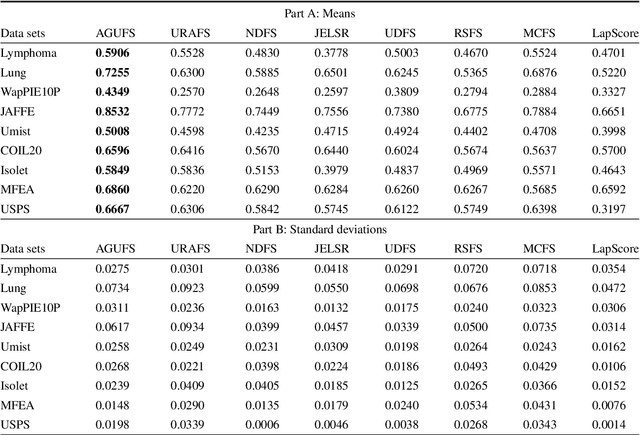
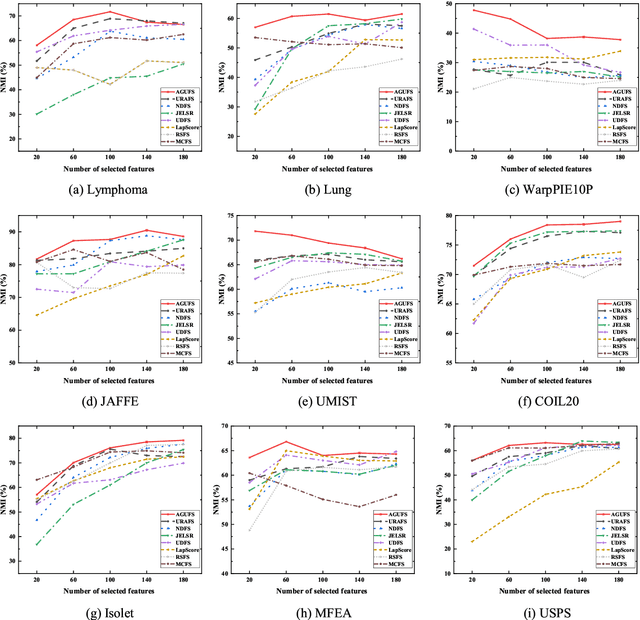
Unsupervised feature selection is an important method to reduce dimensions of high dimensional data without labels, which is benefit to avoid ``curse of dimensionality'' and improve the performance of subsequent machine learning tasks, like clustering and retrieval. How to select the uncorrelated and discriminative features is the key problem of unsupervised feature selection. Many proposed methods select features with strong discriminant and high redundancy, or vice versa. However, they only satisfy one of these two criteria. Other existing methods choose the discriminative features with low redundancy by constructing the graph matrix on the original feature space. Since the original feature space usually contains redundancy and noise, it will degrade the performance of feature selection. In order to address these issues, we first present a novel generalized regression model imposed by an uncorrelated constraint and the $\ell_{2,1}$-norm regularization. It can simultaneously select the uncorrelated and discriminative features as well as reduce the variance of these data points belonging to the same neighborhood, which is help for the clustering task. Furthermore, the local intrinsic structure of data is constructed on the reduced dimensional space by learning the similarity-induced graph adaptively. Then the learnings of the graph structure and the indicator matrix based on the spectral analysis are integrated into the generalized regression model. Finally, we develop an alternative iterative optimization algorithm to solve the objective function. A series of experiments are carried out on nine real-world data sets to demonstrate the effectiveness of the proposed method in comparison with other competing approaches.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge