Adaptive Granularity in Tensors: A Quest for Interpretable Structure

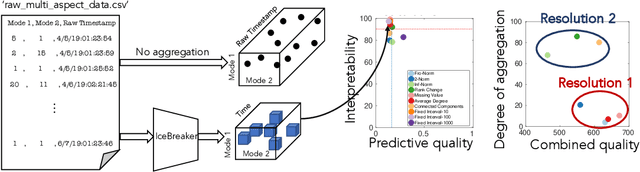
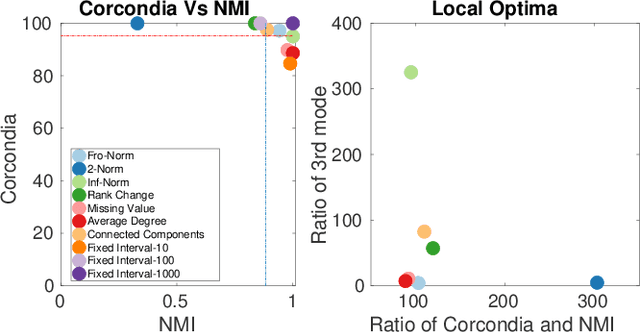
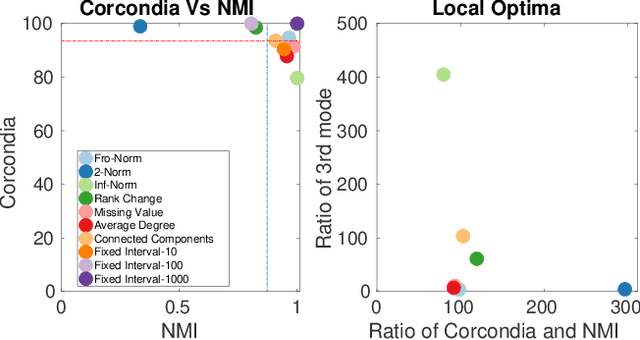
Data collected at very frequent intervals is usually extremely sparse and has no structure that is exploitable by modern tensor decomposition algorithms. Thus the utility of such tensors is low, in terms of the amount of interpretable and exploitable structure that one can extract from them. In this paper, we introduce the problem of finding a tensor of adaptive aggregated granularity that can be decomposed to reveal meaningful latent concepts (structures) from datasets that, in their original form, are not amenable to tensor analysis. Such datasets fall under the broad category of sparse point processes that evolve over space and/or time. To the best of our knowledge, this is the first work that explores adaptive granularity aggregation in tensors. Furthermore, we formally define the problem and discuss what different definitions of "good structure" can be in practice, and show that optimal solution is of prohibitive combinatorial complexity. Subsequently, we propose an efficient and effective greedy algorithm which follows a number of intuitive decision criteria that locally maximize the "goodness of structure", resulting in high-quality tensors. We evaluate our method on both semi-synthetic data where ground truth is known and real datasets for which we do not have any ground truth. In both cases, our proposed method constructs tensors that have very high structure quality. Finally, our proposed method is able to discover different natural resolutions of a multi-aspect dataset, which can lead to multi-resolution analysis.