Adaptive Affinity Matrix for Unsupervised Metric Learning
Paper and Code
Sep 11, 2016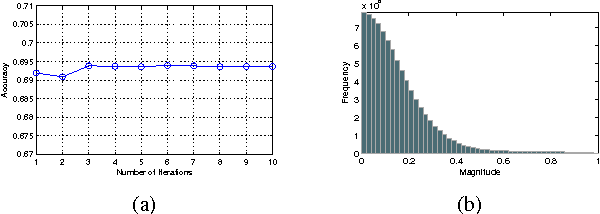

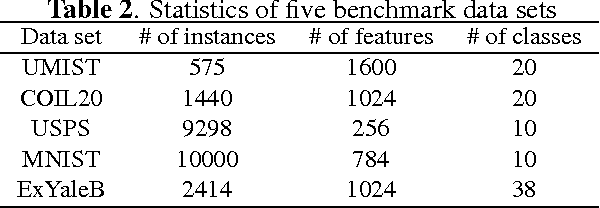
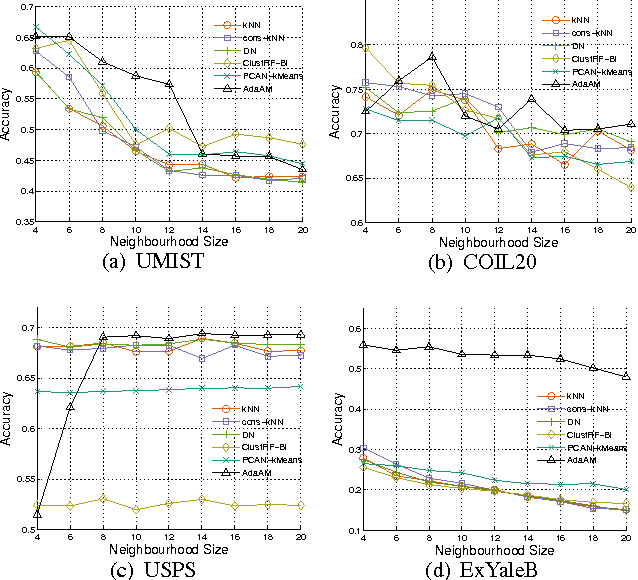
Spectral clustering is one of the most popular clustering approaches with the capability to handle some challenging clustering problems. Most spectral clustering methods provide a nonlinear map from the data manifold to a subspace. Only a little work focuses on the explicit linear map which can be viewed as the unsupervised distance metric learning. In practice, the selection of the affinity matrix exhibits a tremendous impact on the unsupervised learning. While much success of affinity learning has been achieved in recent years, some issues such as noise reduction remain to be addressed. In this paper, we propose a novel method, dubbed Adaptive Affinity Matrix (AdaAM), to learn an adaptive affinity matrix and derive a distance metric from the affinity. We assume the affinity matrix to be positive semidefinite with ability to quantify the pairwise dissimilarity. Our method is based on posing the optimization of objective function as a spectral decomposition problem. We yield the affinity from both the original data distribution and the widely-used heat kernel. The provided matrix can be regarded as the optimal representation of pairwise relationship on the manifold. Extensive experiments on a number of real-world data sets show the effectiveness and efficiency of AdaAM.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge