Active Learning with Label Comparisons
Paper and Code
Apr 10, 2022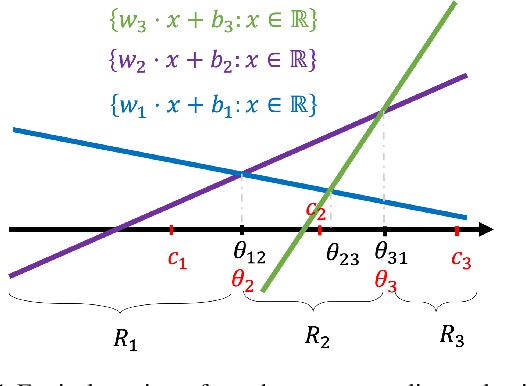
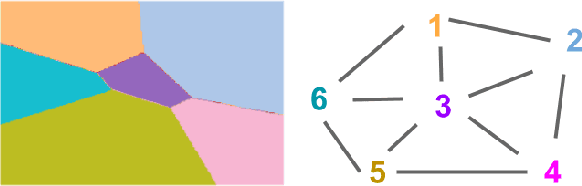
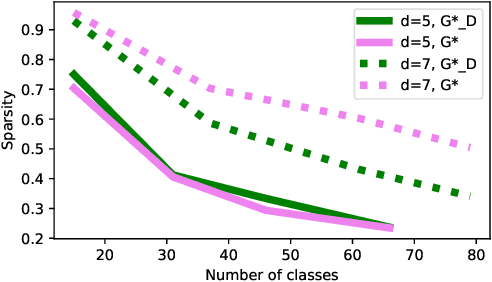
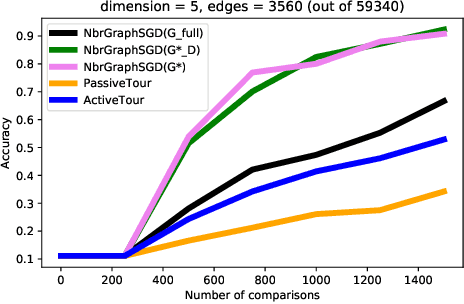
Supervised learning typically relies on manual annotation of the true labels. When there are many potential classes, searching for the best one can be prohibitive for a human annotator. On the other hand, comparing two candidate labels is often much easier. We focus on this type of pairwise supervision and ask how it can be used effectively in learning, and in particular in active learning. We obtain several insightful results in this context. In principle, finding the best of $k$ labels can be done with $k-1$ active queries. We show that there is a natural class where this approach is sub-optimal, and that there is a more comparison-efficient active learning scheme. A key element in our analysis is the "label neighborhood graph" of the true distribution, which has an edge between two classes if they share a decision boundary. We also show that in the PAC setting, pairwise comparisons cannot provide improved sample complexity in the worst case. We complement our theoretical results with experiments, clearly demonstrating the effect of the neighborhood graph on sample complexity.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge