Active and Adaptive Sequential learning

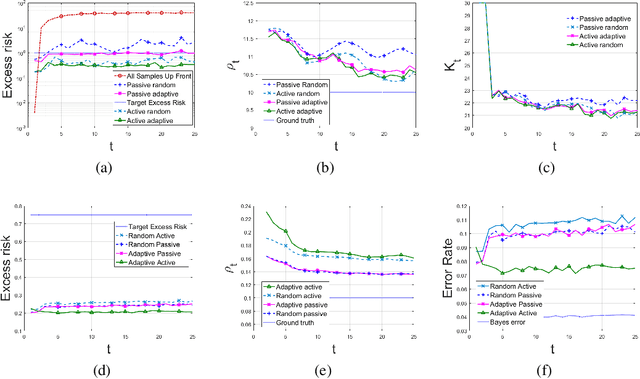
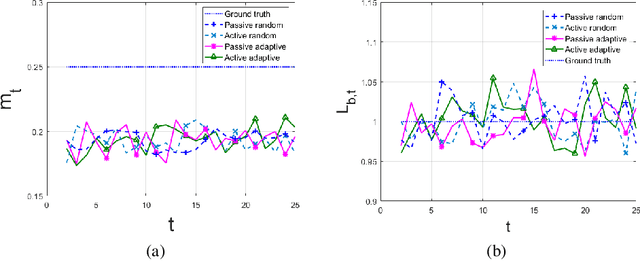
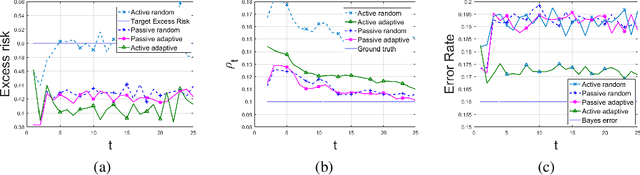
A framework is introduced for actively and adaptively solving a sequence of machine learning problems, which are changing in bounded manner from one time step to the next. An algorithm is developed that actively queries the labels of the most informative samples from an unlabeled data pool, and that adapts to the change by utilizing the information acquired in the previous steps. Our analysis shows that the proposed active learning algorithm based on stochastic gradient descent achieves a near-optimal excess risk performance for maximum likelihood estimation. Furthermore, an estimator of the change in the learning problems using the active learning samples is constructed, which provides an adaptive sample size selection rule that guarantees the excess risk is bounded for sufficiently large number of time steps. Experiments with synthetic and real data are presented to validate our algorithm and theoretical results.