ACORN: Adaptive Coordinate Networks for Neural Scene Representation
Paper and Code
May 06, 2021
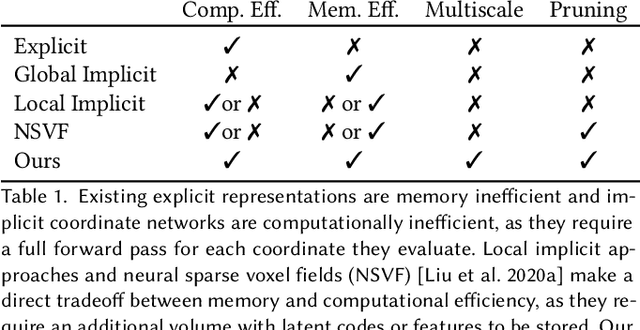
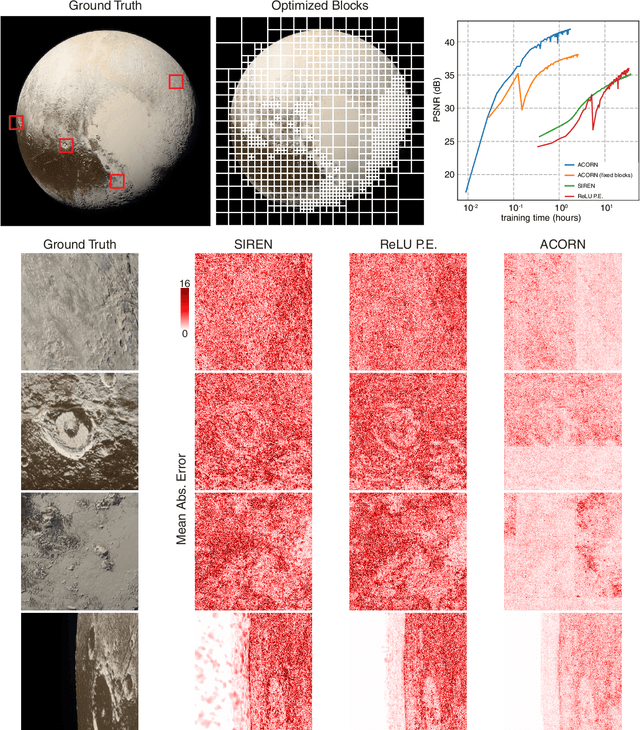
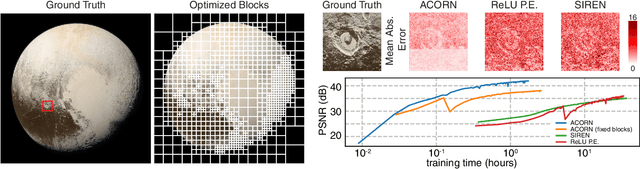
Neural representations have emerged as a new paradigm for applications in rendering, imaging, geometric modeling, and simulation. Compared to traditional representations such as meshes, point clouds, or volumes they can be flexibly incorporated into differentiable learning-based pipelines. While recent improvements to neural representations now make it possible to represent signals with fine details at moderate resolutions (e.g., for images and 3D shapes), adequately representing large-scale or complex scenes has proven a challenge. Current neural representations fail to accurately represent images at resolutions greater than a megapixel or 3D scenes with more than a few hundred thousand polygons. Here, we introduce a new hybrid implicit-explicit network architecture and training strategy that adaptively allocates resources during training and inference based on the local complexity of a signal of interest. Our approach uses a multiscale block-coordinate decomposition, similar to a quadtree or octree, that is optimized during training. The network architecture operates in two stages: using the bulk of the network parameters, a coordinate encoder generates a feature grid in a single forward pass. Then, hundreds or thousands of samples within each block can be efficiently evaluated using a lightweight feature decoder. With this hybrid implicit-explicit network architecture, we demonstrate the first experiments that fit gigapixel images to nearly 40 dB peak signal-to-noise ratio. Notably this represents an increase in scale of over 1000x compared to the resolution of previously demonstrated image-fitting experiments. Moreover, our approach is able to represent 3D shapes significantly faster and better than previous techniques; it reduces training times from days to hours or minutes and memory requirements by over an order of magnitude.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge