Achieving Representative Data via Convex Hull Feasibility Sampling Algorithms
Paper and Code
Apr 13, 2022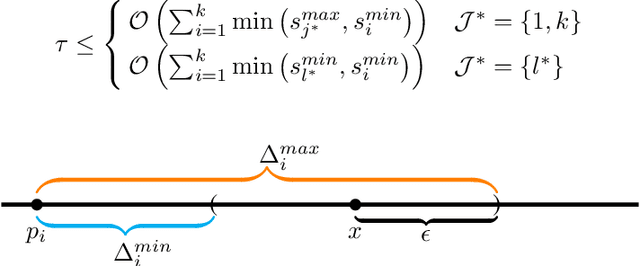


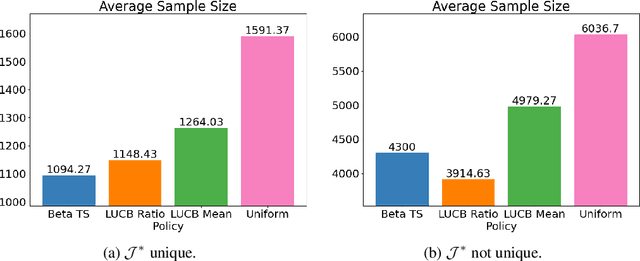
Sampling biases in training data are a major source of algorithmic biases in machine learning systems. Although there are many methods that attempt to mitigate such algorithmic biases during training, the most direct and obvious way is simply collecting more representative training data. In this paper, we consider the task of assembling a training dataset in which minority groups are adequately represented from a given set of data sources. In essence, this is an adaptive sampling problem to determine if a given point lies in the convex hull of the means from a set of unknown distributions. We present adaptive sampling methods to determine, with high confidence, whether it is possible to assemble a representative dataset from the given data sources. We also demonstrate the efficacy of our policies in simulations in the Bernoulli and a multinomial setting.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge