Achievable Rate Maximization for Underlay Spectrum Sharing MIMO System with Intelligent Reflecting Surface
Paper and Code
Dec 21, 2021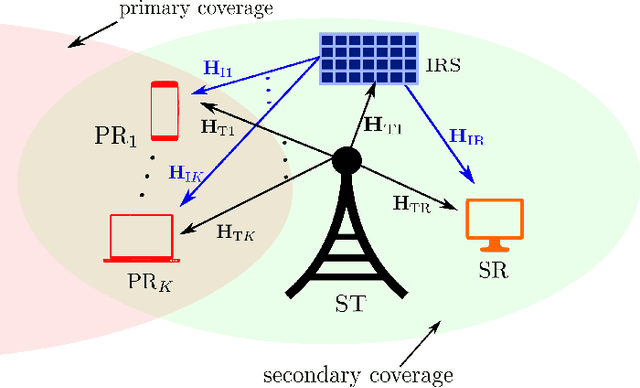
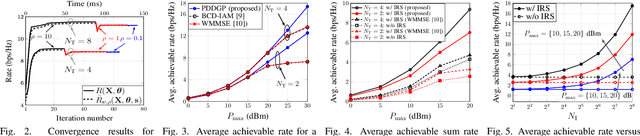
We consider the achievable rate maximization problem for intelligent reflecting surface (IRS) assisted multiple-input multiple-output systems in an underlay spectrum sharing scenario, subject to interference power constraints at primary users. The formulated non-convex optimization problem is challenging to solve due to its non-convexity as well as coupling design variables in the constraints. Different from existing works that are mostly based on alternating optimization (AO), we propose a penalty dual decomposition based gradient projection (PDDGP) algorithm to solve this problem. We also provide a convergence proof and a complexity analysis for the proposed algorithm. We benchmark the proposed algorithm against two known solutions, namely a minimum mean-square error based AO algorithm and an inner approximation method with block coordinate descent. Specifically, the complexity of the proposed algorithm is $O(N_I^2)$ while that of the two benchmark methods is $O(N_I^3)$, where $N_I$ is the number of IRS elements. Moreover, numerical results show that the proposed PDDGP algorithm yields considerably higher achievable rate than the benchmark solutions.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge