Accounting for Missing Covariates in Heterogeneous Treatment Estimation
Paper and Code
Oct 21, 2024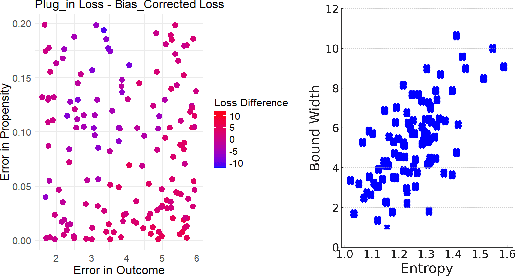
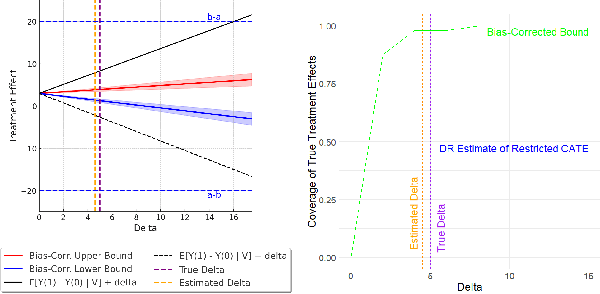
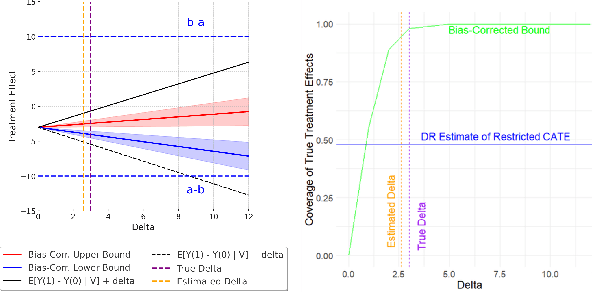
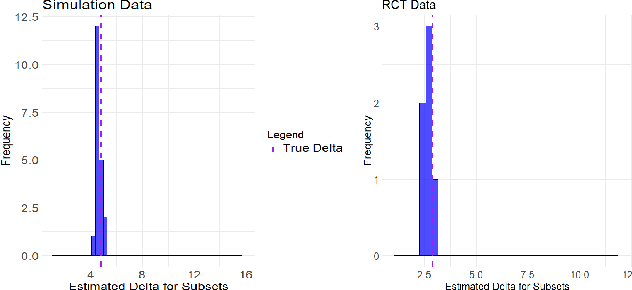
Many applications of causal inference require using treatment effects estimated on a study population to make decisions in a separate target population. We consider the challenging setting where there are covariates that are observed in the target population that were not seen in the original study. Our goal is to estimate the tightest possible bounds on heterogeneous treatment effects conditioned on such newly observed covariates. We introduce a novel partial identification strategy based on ideas from ecological inference; the main idea is that estimates of conditional treatment effects for the full covariate set must marginalize correctly when restricted to only the covariates observed in both populations. Furthermore, we introduce a bias-corrected estimator for these bounds and prove that it enjoys fast convergence rates and statistical guarantees (e.g., asymptotic normality). Experimental results on both real and synthetic data demonstrate that our framework can produce bounds that are much tighter than would otherwise be possible.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge