Accelerating MCMC via Parallel Predictive Prefetching
Paper and Code
Mar 28, 2014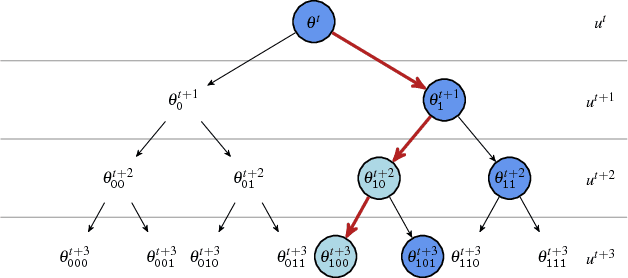
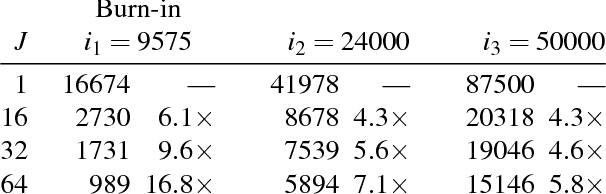


We present a general framework for accelerating a large class of widely used Markov chain Monte Carlo (MCMC) algorithms. Our approach exploits fast, iterative approximations to the target density to speculatively evaluate many potential future steps of the chain in parallel. The approach can accelerate computation of the target distribution of a Bayesian inference problem, without compromising exactness, by exploiting subsets of data. It takes advantage of whatever parallel resources are available, but produces results exactly equivalent to standard serial execution. In the initial burn-in phase of chain evaluation, it achieves speedup over serial evaluation that is close to linear in the number of available cores.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge