Accelerating Ill-Conditioned Low-Rank Matrix Estimation via Scaled Gradient Descent

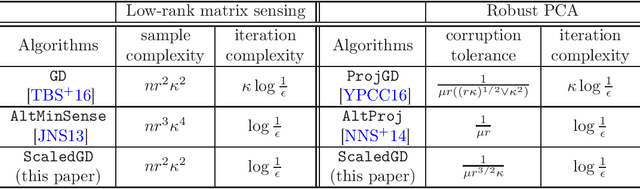
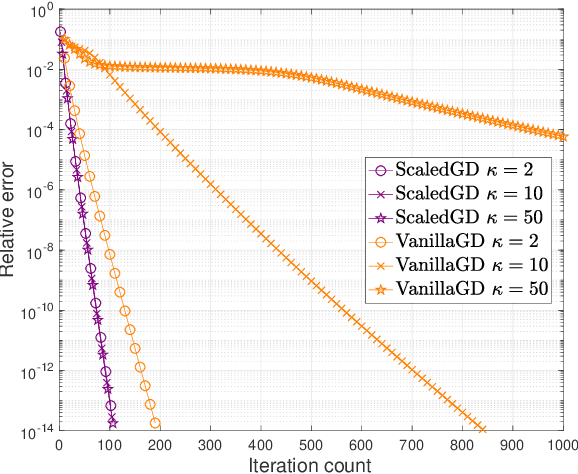
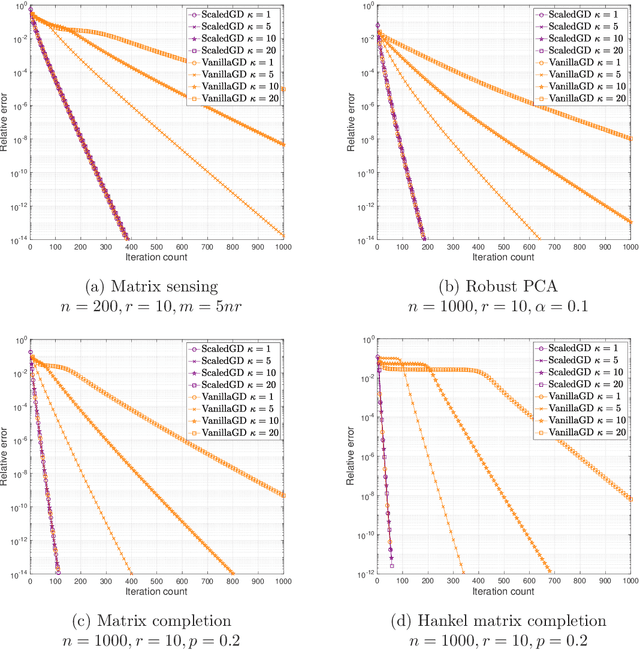
Low-rank matrix estimation is a canonical problem that finds numerous applications in signal processing, machine learning and imaging science. A popular approach in practice is to factorize the matrix into two compact low-rank factors, and then seek to optimize these factors directly via simple iterative methods such as gradient descent and alternating minimization. Despite nonconvexity, recent literatures have shown that these simple heuristics in fact achieve linear convergence when initialized properly for a growing number of problems of interest. However, upon closer examination, existing approaches can still be computationally expensive especially for ill-conditioned matrices: the convergence rate of gradient descent depends linearly on the condition number of the low-rank matrix, while the per-iteration cost of alternating minimization is often prohibitive for large matrices. The goal of this paper is to set forth a new algorithmic approach dubbed Scaled Gradient Descent (ScaledGD) which can be viewed as pre-conditioned or diagonally-scaled gradient descent, where the pre-conditioners are adaptive and iteration-varying with a minimal computational overhead. For low-rank matrix sensing and robust principal component analysis, we theoretically show that ScaledGD achieves the best of both worlds: it converges linearly at a rate independent of the condition number similar as alternating minimization, while maintaining the low per-iteration cost of gradient descent. To the best of our knowledge, ScaledGD is the first algorithm that provably has such properties. At the core of our analysis is the introduction of a new distance function that takes account of the pre-conditioners when measuring the distance between the iterates and the ground truth.