Accelerating Eulerian Fluid Simulation With Convolutional Networks
Paper and Code
Jun 22, 2017
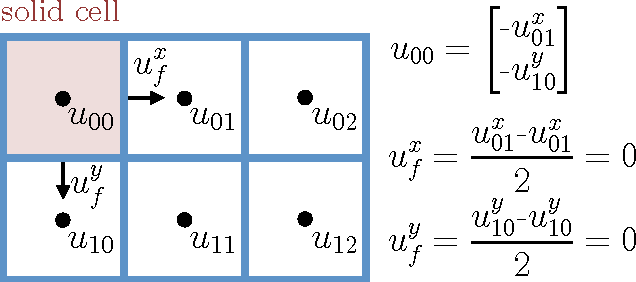
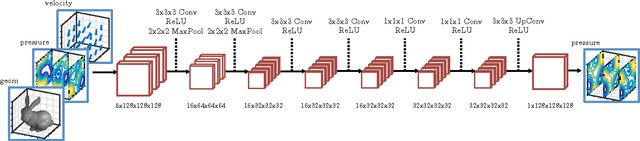
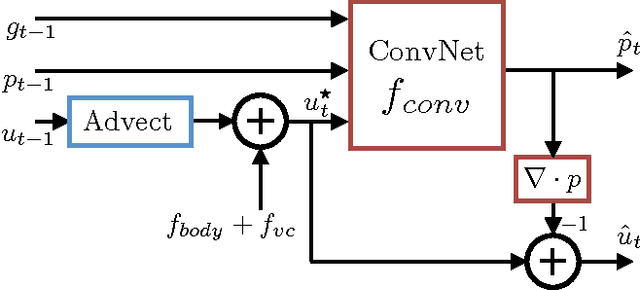
Efficient simulation of the Navier-Stokes equations for fluid flow is a long standing problem in applied mathematics, for which state-of-the-art methods require large compute resources. In this work, we propose a data-driven approach that leverages the approximation power of deep-learning with the precision of standard solvers to obtain fast and highly realistic simulations. Our method solves the incompressible Euler equations using the standard operator splitting method, in which a large sparse linear system with many free parameters must be solved. We use a Convolutional Network with a highly tailored architecture, trained using a novel unsupervised learning framework to solve the linear system. We present real-time 2D and 3D simulations that outperform recently proposed data-driven methods; the obtained results are realistic and show good generalization properties.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge