Accelerated First-order Methods on the Wasserstein Space for Bayesian Inference

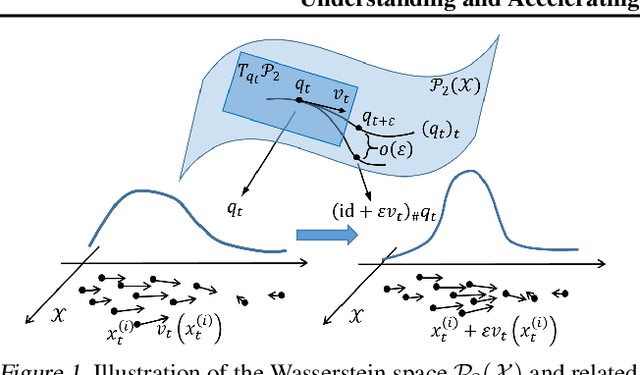
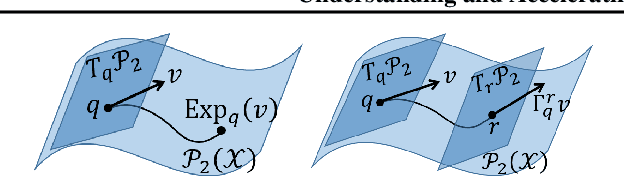
We consider doing Bayesian inference by minimizing the KL divergence on the 2-Wasserstein space $\mathcal{P}_2$. By exploring the Riemannian structure of $\mathcal{P}_2$, we develop two inference methods by simulating the gradient flow on $\mathcal{P}_2$ via updating particles, and an acceleration method that speeds up all such particle-simulation-based inference methods. Moreover we analyze the approximation flexibility of such methods, and conceive a novel bandwidth selection method for the kernel that they use. We note that $\mathcal{P}_2$ is quite abstract and general so that our methods can make closer approximation, while it still has a rich structure that enables practical implementation. Experiments show the effectiveness of the two proposed methods and the improvement of convergence by the acceleration method.