A Winning Hand: Compressing Deep Networks Can Improve Out-Of-Distribution Robustness
Paper and Code
Jun 16, 2021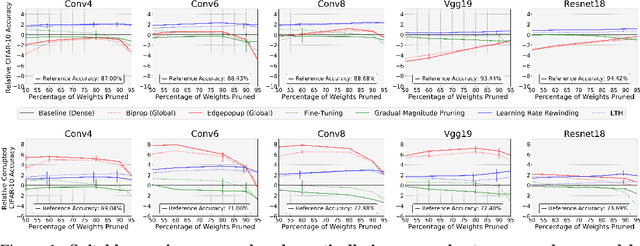
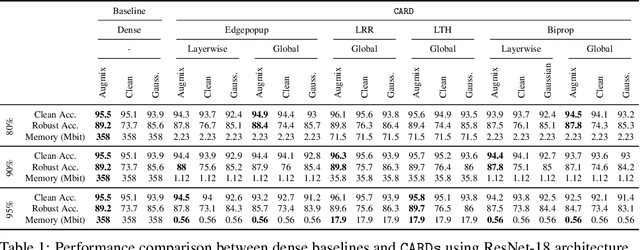
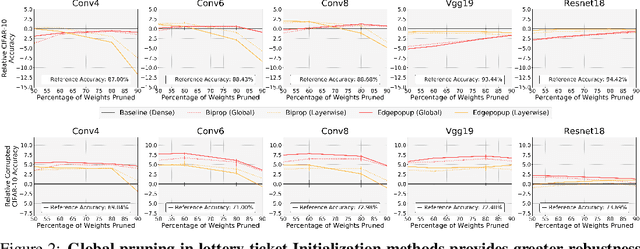
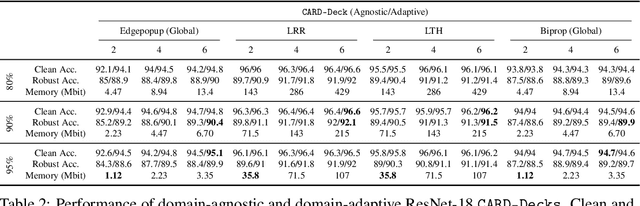
Two crucial requirements for a successful adoption of deep learning (DL) in the wild are: (1) robustness to distributional shifts, and (2) model compactness for achieving efficiency. Unfortunately, efforts towards simultaneously achieving Out-of-Distribution (OOD) robustness and extreme model compactness without sacrificing accuracy have mostly been unsuccessful. This raises an important question: "Is the inability to create compact, accurate, and robust deep neural networks (CARDs) fundamental?" To answer this question, we perform a large-scale analysis for a range of popular model compression techniques which uncovers several intriguing patterns. Notably, in contrast to traditional pruning approaches (e.g., fine tuning and gradual magnitude pruning), we find that "lottery ticket-style" pruning approaches can surprisingly be used to create high performing CARDs. Specifically, we are able to create extremely compact CARDs that are dramatically more robust than their significantly larger and full-precision counterparts while matching (or beating) their test accuracy, simply by pruning and/or quantizing. To better understand these differences, we perform sensitivity analysis in the Fourier domain for CARDs trained using different data augmentation methods. Motivated by our analysis, we develop a simple domain-adaptive test-time ensembling approach (CARD-Deck) that uses a gating module to dynamically select an appropriate CARD from the CARD-Deck based on their spectral-similarity with test samples. By leveraging complementary frequency biases of different compressed models, the proposed approach builds a "winning hand" of CARDs that establishes a new state-of-the-art on CIFAR-10-C accuracies (i.e., 96.8% clean and 92.75% robust) with dramatically better memory usage than their non-compressed counterparts. We also present some theoretical evidences supporting our empirical findings.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge