A Variational Perspective on Generative Flow Networks
Paper and Code
Oct 14, 2022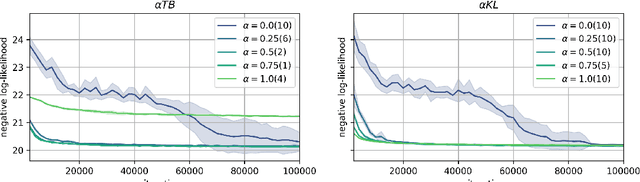
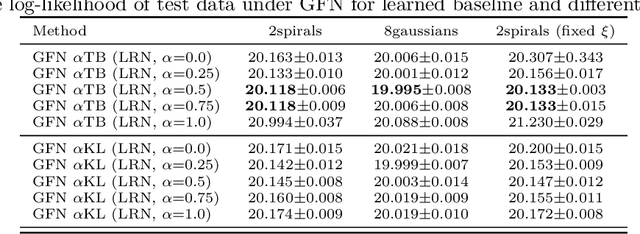
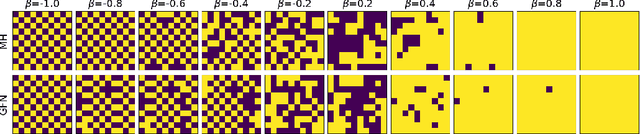

Generative flow networks (GFNs) are a class of models for sequential sampling of composite objects, which approximate a target distribution that is defined in terms of an energy function or a reward. GFNs are typically trained using a flow matching or trajectory balance objective, which matches forward and backward transition models over trajectories. In this work, we define variational objectives for GFNs in terms of the Kullback-Leibler (KL) divergences between the forward and backward distribution. We show that variational inference in GFNs is equivalent to minimizing the trajectory balance objective when sampling trajectories from the forward model. We generalize this approach by optimizing a convex combination of the reverse- and forward KL divergence. This insight suggests variational inference methods can serve as a means to define a more general family of objectives for training generative flow networks, for example by incorporating control variates, which are commonly used in variational inference, to reduce the variance of the gradients of the trajectory balance objective. We evaluate our findings and the performance of the proposed variational objective numerically by comparing it to the trajectory balance objective on two synthetic tasks.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge